
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,已知點
,已知點![]() .
.
(1)求出點![]() ,點
,點![]() 的坐標.
的坐標.
(2)![]() 是直線
是直線![]() 上一動點,且
上一動點,且![]() 和
和![]() 的面積相等,求點
的面積相等,求點![]() 坐標.
坐標.
(3)如圖2,平移直線![]() ,分別交
,分別交![]() 軸,
軸,![]() 軸于交于點
軸于交于點![]() ,
,![]() ,過點
,過點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,在直線
,在直線![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 是等腰直角三角形?若存在,請直接寫出所有符合條件的點
是等腰直角三角形?若存在,請直接寫出所有符合條件的點![]() 的坐標.
的坐標.
圖1 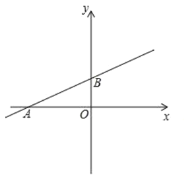 圖2
圖2 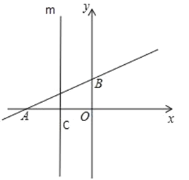
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
![]() .
.
【解析】
(1)根據A,B坐標的特點即可求解;
(2)分P點在線段AB上、直線AB上根據三角形的面積公式即可求解;
(3)設Q(-2,t),分別求出AB2,AQ2,BQ2,根據等腰三角形的性質分情況討論即可求解.
(1)令y=![]() =0,解得x=-4,
=0,解得x=-4,
∴A(-4,0)
令x=0,y=![]() =2,
=2,
∴B(0,2)
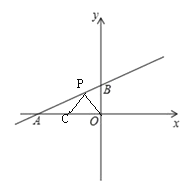
(2)如圖,當P點在線段AB上,設P(x,![]() )
)
∵![]() ,A(-4,0),B(0,2)
,A(-4,0),B(0,2)
∴CO=2=OB,OA=4
∵![]() 和
和![]() 的面積相等
的面積相等
∴![]() BO×(-x)=
BO×(-x)= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×(-x)=
×2×(-x)= ![]() ×2×(
×2×(![]() )
)
解得x=![]()
∴![]()
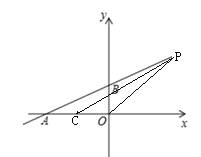
如圖,當P點在直線AB上,當P在BA的延長線上,S△BOP>S△COP
故P在AB的延長線上,
設P(x,![]() )
)
∵![]() 和
和![]() 的面積相等
的面積相等
∴![]() BO×x=
BO×x= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×x=
×2×x= ![]() ×2×(
×2×(![]() )
)
解得x=4
∴![]()
綜上,![]() 或
或![]() ;
;
(3)∵過點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,點
,點![]() 在直線
在直線![]() 上是
上是
∴設Q(-2,t),
∵A(-4,0),B(0,2)
∴AB2=20,AQ2=22+t2=4+t2,BQ2=22+(2-t)2=4+(2-t)2,
故當AB=BQ,即20=4+(2-t)2,
解得:t=-2或t=6
故Q![]()
故當AB=AQ,即20=4+t2,
解得:t=±4
故![]()
當AQ=BQ,即4+t2=4+(2-t)2,
解得:t=1
∵(-2,1)在直線y=![]() 上,故舍去
上,故舍去
∴Q點坐標為:![]()
![]() .
.


科目:初中數學 來源: 題型:
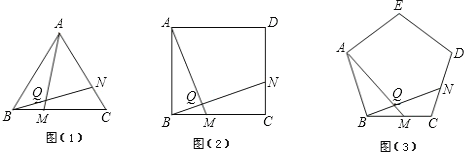
【題目】(1)如圖(1),已知△ABC為正三角形,點M是BC上一點,點N是AC上一點,AM、BN相交于點Q,BM=CN.求出∠BQM的度數;
(2)將(1)中的“正△ABC”分別改為正方形ABCD、正五邊形ABCDE、…正n邊形ABCD…,“點N是AC上一點”改為點N是CD上一點,其余條件不變,分別推斷出∠BQM等于多少度,將結論填入下表:
正多邊形 | 正方形 | 正五邊形 | …… | 正n邊形 |
∠BQM的度數 |
|
| …… |
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 上一點,
上一點,![]() ,連接
,連接![]() ,
,![]() ,
,![]() .
.
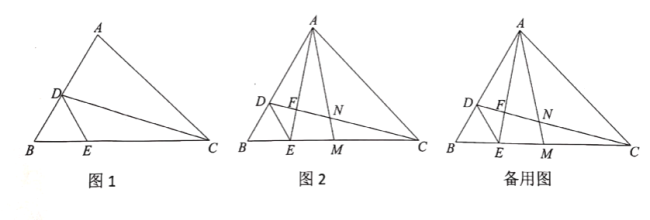
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,連接![]() 交
交![]() 于點
于點![]() ,點
,點![]() 為
為![]() 上一點,連接
上一點,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,若![]() ,直接寫出線段
,直接寫出線段![]() ,
,![]() ,
,![]() 的等量關系.
的等量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩個不透明的布袋,甲袋中有2個完全相同的小球,分別標有數字0和-2;乙袋中有3個完全相同的小球,分別標有數字-2,0和1,小明從甲袋中隨機取出1個小球,記錄標有的數字為x,再從乙袋中隨機取出1個小球,記錄標有的數字為y,這樣確定了點Q的坐標(x,y).
(1)寫出點Q所有可能的坐標;
(2)求點Q在x軸上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一條直線上有兩只螞蟻,甲螞蟻在點A處,乙螞蟻在點B處,假設兩只螞蟻同時出發,爬行方向只能沿直線AB在“向左”或“向右”中隨機選擇,并且甲螞蟻爬行的速度比乙螞蟻快.(1)甲螞蟻選擇“向左”爬行的概率為________;
(2)利用列表或畫樹狀圖的方法求兩只螞蟻開始爬行后會“觸碰到”的概率.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),一架云梯AB斜靠在一豎直的墻上,云梯的頂端A距地面15米,梯子的長度比梯子底端B離墻的距離大5米.
(1)這個云梯的底端B離墻多遠?
(2)如圖(2),如果梯子的頂端下滑了8m(AC的長),那么梯子的底部在水平方向右滑動了多少米?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網絡約車公司近期推出了“520專享”服務計劃,即要求公司員工做到“5星級服務、2分鐘響應、0客戶投訴”,為進一步提升服務品質,公司監管部門決定了解“單次營運里程”的分布情況.老王收集了本公司的5 000個“單次營運里程”數據,這些里程數據均不超過25(公里),他從中隨機抽取了200個數據作為一個樣本,整理、統計結果如下表,并繪制了不完整的頻數分布直方圖.
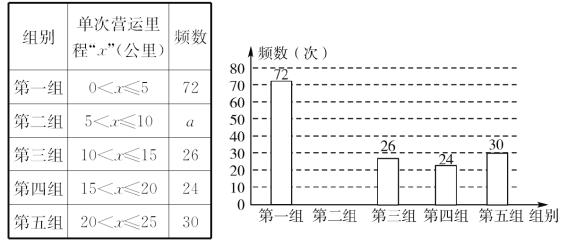
根據統計表、圖提供的信息,解答下面的問題:
(1)表中a=________;樣本中“單次營運里程”不超過15公里的頻率為________;(2)請把頻數分布直方圖補充完整;
(3)請估計該公司這5 000個“單次營運里程”超過20公里的次數;
查看答案和解析>>
科目:初中數學 來源: 題型:
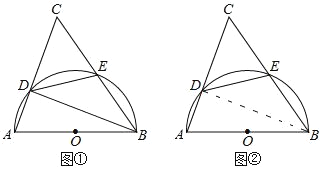
【題目】已知,△ABC中,∠A=68°,以AB為直徑的⊙O與AC,BC的交點分別為D,E
(Ⅰ)如圖①,求∠CED的大小;
(Ⅱ)如圖②,當DE=BE時,求∠C的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com