
【題目】![]() 嘗試探究
嘗試探究
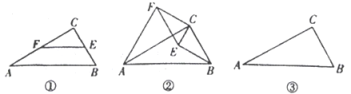
如圖-![]() ,在△ABC中,∠C=90°,∠A=30°,點E、F分別是BC、AC邊上的點,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,點E、F分別是BC、AC邊上的點,且EF//BC.
![]()
![]() 的值為 ;
的值為 ;![]() 直線
直線![]() 與直線
與直線![]() 的位置關系為 ;
的位置關系為 ;
![]() 類比延伸
類比延伸
如圖![]() ,若將圖
,若將圖![]() 中的
中的![]() 繞點
繞點![]() 順時針旋轉,連接
順時針旋轉,連接![]() ,則在旋轉的過程中,請判斷
,則在旋轉的過程中,請判斷![]() 的值及直線
的值及直線![]() 與直
與直![]() 線的位置關系,并說明理由;
線的位置關系,并說明理由;
![]() 拓展運用
拓展運用
若![]() ,在旋轉過程中,當
,在旋轉過程中,當![]() 三點在同一直線上時,請直接寫出此時線段
三點在同一直線上時,請直接寫出此時線段![]() 的長.
的長.
【答案】![]()
![]()
![]() ;
;![]()
![]() ;
;![]()
![]()
![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①根據直角三角形30°角的性質即可解決問題;
②根據已知可直接得出答案;
(2)只要證明△ACF△BCE,根據相似三角形的性質即可得![]() 的值,也可得∠BCE=∠CAF,繼而推導
的值,也可得∠BCE=∠CAF,繼而推導![]() 即可得;
即可得;
(3)分兩種情況畫出圖形分別解決即可.
![]() ①∵在△ABC中,∠ABC=90°,∠A=30°,EF//AB,
①∵在△ABC中,∠ABC=90°,∠A=30°,EF//AB,
∴∠CFE=∠A=30°,
∴CF=![]() =
=![]() EC,AC=
EC,AC=![]() =
=![]() BC,
BC,
∴AF=AC-CF=![]() BC-
BC-![]() EC=
EC=![]() (BC-EC)=
(BC-EC)=![]() BE,
BE,
∴![]() =
=![]() ,
,
故答案為:![]() ;
;
②∵∠ACB=90°,
∴![]() ,即直線
,即直線![]() 與直線
與直線![]() 的位置關系為垂直,
的位置關系為垂直,
故答案為:![]() ;
;
![]()
![]()
![]() ,
,
理由如下:由![]() 及旋轉的性質知
及旋轉的性質知![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,
∴![]() =
=![]()
![]() ,
,
![]() ,
,
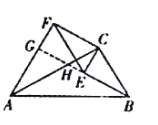
如圖,延長![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() ;
;
![]() ①如圖,∵△ECB∽△FCA,∴AF:BE=CF:CE=
①如圖,∵△ECB∽△FCA,∴AF:BE=CF:CE=![]() ,
,
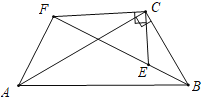
設BE=a,則AF=![]() a,
a,
∵B、E、F共線,∴∠BEC=∠AFC=120°,
∵∠EFC=30°,∴∠AFB=90°,
在Rt△ABF中,AB=2BC=6,AF=![]() a,BF=EF+BE=4+a,
a,BF=EF+BE=4+a,
∴![]() ,
,
∴a=-1+![]() 或-1-
或-1-![]() (舍去),
(舍去),
∴AF=![]() a=
a=![]() ;
;
②如圖,當E、B、F共線時,同法可證:AF=![]() BE,∠AFB=90°,
BE,∠AFB=90°,
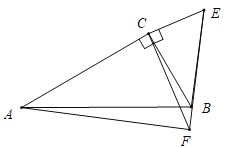
在Rt△ABF中,![]() ,
,
∴a=1+![]() 或1-
或1-![]() (舍去),
(舍去),
∴AF=![]() a=
a=![]() ,
,
綜上,AF的長為![]() 或
或![]() .
.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中數學 來源: 題型:
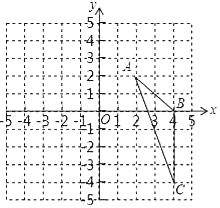
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別是A(2,2),B(4,0),C(4,﹣4).
(1)請在圖中,畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(2)以點O為位似中心,將△ABC縮小為原來的![]() ,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中數學 來源: 題型:
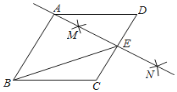
【題目】如圖,在菱形![]() 中,
中,![]() ,按以下步驟作圖:①分別以點
,按以下步驟作圖:①分別以點![]() 和點
和點![]() 為圓心,為圓心,大于號
為圓心,為圓心,大于號![]() 的長為半徑面狐,兩弧交于點
的長為半徑面狐,兩弧交于點![]() ,
,![]() :②做直線
:②做直線![]() ,且
,且![]() 恰好經過點
恰好經過點![]() ,與
,與![]() 交于點
交于點![]() ,連接
,連接![]() ,則
,則![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
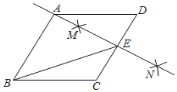
【題目】如圖,在菱形![]() 中,
中,![]() ,按以下步驟作圖:①分別以點
,按以下步驟作圖:①分別以點![]() 和點
和點![]() 為圓心,為圓心,大于號
為圓心,為圓心,大于號![]() 的長為半徑面狐,兩弧交于點
的長為半徑面狐,兩弧交于點![]() ,
,![]() :②做直線
:②做直線![]() ,且
,且![]() 恰好經過點
恰好經過點![]() ,與
,與![]() 交于點
交于點![]() ,連接
,連接![]() ,則
,則![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
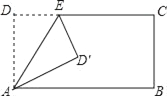
【題目】如圖,矩形ABCD中,AD=5,AB=8,點E為DC上一個動點,把△ADE沿AE折疊,若點D的對應點D′,連接D′B,以下結論中:①D′B的最小值為3;②當DE=![]() 時,△ABD′是等腰三角形;③當DE=2是,△ABD′是直角三角形;④△ABD′不可能是等腰直角三角形;其中正確的有_____.(填上你認為正確結論的序號)
時,△ABD′是等腰三角形;③當DE=2是,△ABD′是直角三角形;④△ABD′不可能是等腰直角三角形;其中正確的有_____.(填上你認為正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某鄉鎮實施產業精準扶貧,幫助貧困戶承包了若干畝土地種植新品草莓,已知該草莓的成本為每千克10元,草莓成熟后投入市場銷售,經市場調查發現,草莓銷售不會虧本,且每天的銷售量y(千克)與銷售單價x(元/千克)之間函數關系如圖所示.

(1)求y與x的函數關系式,并寫出x的取值范圍.
(2)當該品種草莓的定價為多少時,每天銷售獲得利潤最大?最大利潤是多少?
(3)某村今年草莓采摘期限30天,預計產量6000千克,則按照(2)中的方式進行銷售,能否銷售完這批草莓?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 某校為了解九年級男同學的體育考試準備情況,隨機抽取部分男同學進行了1000米跑測試.按照成績分為優秀、良好、合格與不合格四個等級.學校繪制了如下不完整的統計圖.
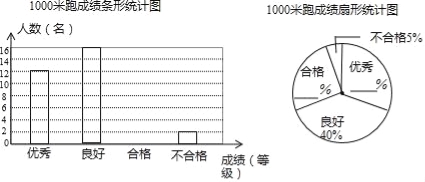
(1)根據給出的信息,補全兩幅統計圖;
(2)該校九年級有600名男生,請估計成績未達到良好有多少名?
(3)某班甲、乙兩位成績優秀的同學被選中參加即將舉行的學校運動會1000米比賽,預賽分為A、B、C三組進行,選手由抽簽確定分組.甲、乙兩人恰好分在同一組的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com