
【題目】如圖,在平面直角坐標系xOy中,直線y=﹣![]() x+
x+![]() 與y=x相交于點A,與x軸交于點B.
與y=x相交于點A,與x軸交于點B.
(1)填空:A的坐標是_______,B的坐標是___________;
(2)直線y=﹣![]() x+
x+![]() 上有點P(m,n),且點P在第四象限,設△AOP的面積為S,請求出S與m的函數關系式;
上有點P(m,n),且點P在第四象限,設△AOP的面積為S,請求出S與m的函數關系式;
(3)在直線OA上,是否存在一點D,使得△DOB是等腰三角形?如果存在,試求出所有符合條件的點D的坐標,如果不存在,請說明理由.
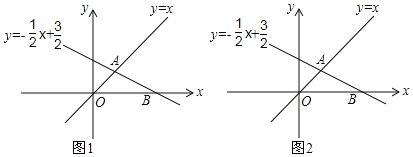
【答案】(1)A(1,1),B(3,0);(2)S=![]() ;(3)存在,D(﹣
;(3)存在,D(﹣![]() ,﹣
,﹣![]() ),D(
),D(![]() ,
,![]() ),D(3,3)或D(
),D(3,3)或D(![]() ,
,![]() ).
).
【解析】
(1)把直線y=-![]() x+
x+![]() 與y=x聯立得出方程組求解即可得出點A的坐標,由直線y=-
與y=x聯立得出方程組求解即可得出點A的坐標,由直線y=-![]() x+
x+![]() 與x軸交于點B,令y=0,求出x的值,即可得出B的坐標;
與x軸交于點B,令y=0,求出x的值,即可得出B的坐標;
(2)根據S = S△AOB+ S△POB即可解答;
(3)在直線OA上,存在一點D,使得△DOB是等腰三角形,分四種情況①當OB=OD時,②當OD=OB時,③當OB=DB時,④當DO=DB時分別求解即可.
解:(1)∵直線y=﹣![]() x+
x+![]() 與y=x相交于點A,
與y=x相交于點A,
∴聯立得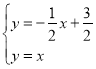 ,解得
,解得![]() ,
,
∴點A(1,1),
∵直線y=﹣![]() x+
x+![]() 與x軸交于點B,
與x軸交于點B,
∴令y=0,得﹣![]() x+
x+![]() =0,解得x=3,
=0,解得x=3,
∴B(3,0).
(2)S=S△AOB+S△OBP=![]()
![]()
(3)在直線OA上,存在一點D,使得△DOB是等腰三角形,
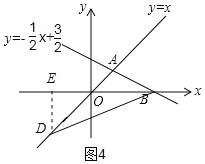
①如圖4,當OB=OD時,作DE⊥x軸,交x軸于點E
∵OB=3,點D在OA上,∠DOE=45°
∴DE=OE=![]() ,
,
∴D(﹣![]() ,﹣
,﹣![]() ),
),
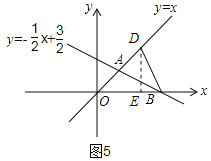
②如圖5,當OD=OB時,作DE⊥x軸,交x軸于點E
∵OB=3,點D在OA上,∠DOE=45°
∴DE=OE=![]() ,
,
∴D(![]() ,
,![]() ),
),
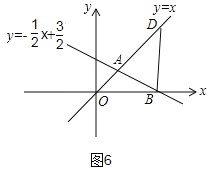
③如圖6,當OB=DB時,
∵∠AOB=∠ODB=45°,
∴DB⊥OB,
∵OB=3,
∴D(3,3),
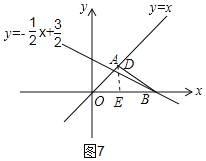
④如圖7,當DO=DB時,作DE⊥x軸,交x軸于點E
∵∠AOB=∠OBD=45°,
∴OD⊥DB,
∵OB=3,
∴OE=![]() ,AE=
,AE=![]() ,
,
∴D(![]() ,
,![]() ).
).
綜上所述,在直線OA上,存在點D(﹣![]() ,﹣
,﹣![]() ),D(
),D(![]() ,
,![]() ),D(3,3)或D(
),D(3,3)或D(![]() ,
,![]() ),使得△DOB是等腰三角形.
),使得△DOB是等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課:樂器、舞蹈、繪畫、書法,學校采取隨機抽樣的方法進行問卷調查![]() 每個被調查的學生必須選擇而且只能選擇其中一門
每個被調查的學生必須選擇而且只能選擇其中一門![]() 對調查結果進行整理,繪制成如下兩幅不完整的統計圖
對調查結果進行整理,繪制成如下兩幅不完整的統計圖![]() 請結合圖中所給信息解答下列問題:
請結合圖中所給信息解答下列問題:


![]() 本次調查的學生共有______人,在扇形統計圖中,m的值是______.
本次調查的學生共有______人,在扇形統計圖中,m的值是______.
![]() 分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
分別求出參加調查的學生中選擇繪畫和書法的人數,并將條形統計圖補充完整.
![]() 該校共有學生2000人,估計該校約有多少人選修樂器課程?
該校共有學生2000人,估計該校約有多少人選修樂器課程?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 中,
中,![]() ,點
,點![]() 為
為![]() 三條角平分線的交點,
三條角平分線的交點,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() ,
,![]() ,則點
,則點![]() 到三邊
到三邊![]() 、
、![]() 、
、![]() 的距離為( )
的距離為( )
A. 2cm,2cm,2cm B. 3cm,3cm,3cm
C. 4cm,4cm,4cm D. 2cm,3cm,5cm
查看答案和解析>>
科目:初中數學 來源: 題型:
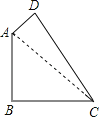
【題目】如圖,在四邊形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=90°,連接AC.
(1)求AC的長度.
(2)求證△ACD是直角三角形.
(3)求四邊形ABCD的面積?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
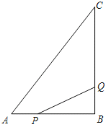
![]() 點
點![]() 從點
從點![]() 開始沿
開始沿![]() 邊向
邊向![]() 以
以![]() 的速度移動,點
的速度移動,點![]() 從
從![]() 點開始沿
點開始沿![]() 邊向點
邊向點![]() 以
以![]() 的速度移動.如果
的速度移動.如果![]() 、
、![]() 分別從
分別從![]() ,
,![]() 同時出發,線段
同時出發,線段![]() 能否將
能否將![]() 分成面積相等的兩部分?若能,求出運動時間;若不能說明理由.
分成面積相等的兩部分?若能,求出運動時間;若不能說明理由.
![]() 若
若![]() 點沿射線
點沿射線![]() 方向從
方向從![]() 點出發以
點出發以![]() 的速度移動,點
的速度移動,點![]() 沿射線
沿射線![]() 方向從
方向從![]() 點出發以
點出發以![]() 的速度移動,
的速度移動,![]() 、
、![]() 同時出發,問幾秒后,
同時出發,問幾秒后,![]() 的面積為
的面積為![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
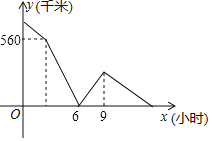
【題目】A、B、C三地在同一直線上,甲、乙兩車分別從A,B兩地相向勻速行駛,甲車先出發2小時,甲車到達B地后立即調頭,并將速度提高10%后與乙車同向行駛,乙車到達A地后,繼續保持原速向遠離B的方向行駛,經過一段時間后兩車同時到達C地,設兩車之間的距離為y(千米),甲行駛的時間x(小時).y與x的關系如圖所示,則B、C兩地相距_____千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC,∠C=90°,AC=12,BC=6,一條線段PQ=AB,P、Q兩點分別在AC和過點A且垂直于AC的射線AX上運動,要使△ABC和△QPA全等,則AP= ______ .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰△ABC中,AB=AC=4cm,∠B=30°,點P從點B出發,以![]() cm/s的速度沿BC方向運動到點C停止,同時點Q從點B出發,以1cm/s的速度沿BA-AC方向運動到點C停止,若△BPQ的面積為y(cm2),運動時間為x(s),求在這一運動過程中y與x之間函數關系式.
cm/s的速度沿BC方向運動到點C停止,同時點Q從點B出發,以1cm/s的速度沿BA-AC方向運動到點C停止,若△BPQ的面積為y(cm2),運動時間為x(s),求在這一運動過程中y與x之間函數關系式.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com