
【題目】已知直線y=kx+b交x軸于點A(1,0) ,與雙曲線![]() 交于點
交于點![]()
(1)求直線AB的解析式為____ ____________;
(2)若 x 軸上存在動點 M(m,0),過點 M 且與 x 軸垂直的直線與直線AB交于點C,與雙曲線交于點D(C、D兩點不重合),當BC >BD時,寫出m的取值范圍_____________.
【答案】(1)y=-x+1;(2)m<-2_或_ m>2
【解析】
(1)將點B(-1,a)代入![]() ,求出a,再將A、B兩點的坐標代入y=kx+b,利用待定系數法即可求出直線AB的解析式;
,求出a,再將A、B兩點的坐標代入y=kx+b,利用待定系數法即可求出直線AB的解析式;
(2)過點B作BE⊥CD于點E.根據三角形中,兩條邊在第三邊上的射影長之間關系,若存在動點M(m,0),滿足BC>BD,則有CE>DE. 由題意得出C(m,-m+1),D(m,![]() ),根據點E與點B的縱坐標相同得到E(m,2),得到CE=
),根據點E與點B的縱坐標相同得到E(m,2),得到CE=![]() , DE=
, DE=![]() ,列不等式,分C在D的上方和C在D的下方兩種情況,數形結合,解不等式即可得其范圍.
,列不等式,分C在D的上方和C在D的下方兩種情況,數形結合,解不等式即可得其范圍.
解:(1)∵點B(-1,a)在雙曲線![]() 上,
上,
∴a=2,
∴B(-1,2).
又∵直線y=kx+b過點A、B,
∴![]() ,
,
解得![]() ,
,
∴直線AB的解析式為:y=-x+1;
(2)
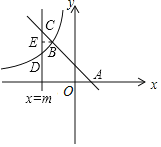
過點B作BE⊥CD于點E.
∵BC>BD,
∴CE>DE
由題意可知,C(m,-m+1),D(m,![]() ),E(m,2),
),E(m,2),
CE=![]() , DE=
, DE=![]() ,
,
∴ ![]() >
>![]()
當m>0時,![]() >
>![]() ,解得m>2,
,解得m>2,
當m<0時,由圖可知,m<-1,又![]() <-(
<-(![]() ),解得m<-2
),解得m<-2
綜上:m<-2或 m>2


科目:初中數學 來源: 題型:
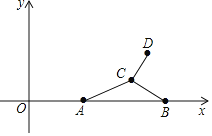
【題目】如圖,在平面直角坐標系中,點A的坐標為(4,0),點B的坐標為(10,0),點C為平面上一動點,連接CA,CB,將線段CB繞點C逆時針旋轉90°得到線段CD,當AC=4,線段AD的長取最大值時,點D的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
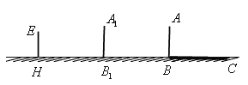
【題目】學習投影后,小明、小穎利用燈光下自己的影子長度來測量一路燈的高度,并探究影子長度的變化規律.如圖,在同一時間,身高為![]() 的小明
的小明![]() 的影子
的影子![]() 長是
長是![]() ,而小穎
,而小穎![]() 剛好在路燈燈泡的正下方
剛好在路燈燈泡的正下方![]() 點,并測得
點,并測得![]() .
.
(1)請在圖中畫出形成影子的光線,并確定路燈燈泡所在的位置![]() ;
;
(2)求路燈燈泡的垂直高度![]() ;
;
(3)如果小明沿線段BH向小穎(點H)走去,當小明走到BH中點B1處時,請在圖中畫出此時小明的影長B1C1,并求B1C1的長;
查看答案和解析>>
科目:初中數學 來源: 題型:
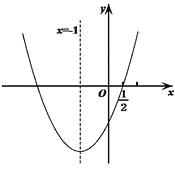
【題目】如圖,二次函數![]() 的圖象經過點
的圖象經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,下列5個結論:①
,下列5個結論:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正確的結論為________________.(注:只填寫正確結論的序號)
,其中正確的結論為________________.(注:只填寫正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
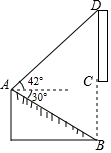
【題目】小婷在放學路上,看到隧道上方有一塊宣傳“中國﹣南亞博覽會”的豎直標語牌CD.她在A點測得標語牌頂端D處的仰角為42°,測得隧道底端B處的俯角為30°(B,C,D在同一條直線上),AB=10m,隧道高6.5m(即BC=65m),求標語牌CD的長(結果保留小數點后一位).(參考數據:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,支付方式的“眾數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com