
【題目】近期江蘇省各地均發布“霧霾”黃色預警,我市某口罩廠商生產一種新型口罩產品,每件制造成本為18元,試銷過程中發現,每月銷售量y(萬件)與銷售單價x(元)之間的關系滿足下表.
銷售單價x(元/件) | … | 20 | 25 | 30 | 40 | … |
每月銷售量y(萬件) | … | 60 | 50 | 40 | 20 | … |
(1)請你從所學過的一次函數、二次函數和反比例函數三個模型中確定哪種函數能比較恰當地表示y與x的變化規律,并直接寫出y與x之間的函數關系式為__________;
(2)當銷售單價為多少元時,廠商每月獲得的利潤為440萬元?
(3)如果廠商每月的制造成本不超過540萬元,那么當銷售單價為多少元時,廠商每月獲得的利潤最大?最大利潤為多少萬元?
【答案】(1)y=﹣2x+100;(2)當銷售單價為28元或40元時,廠商每月獲得的利潤為440萬元;(3)當銷售單價為35元時,廠商每月獲得的利潤最大,最大利潤為510萬元.
【解析】
(1)直接利用待定系數法求出一次函數解析式;
(2)根據利潤=銷售量×(銷售單價﹣成本),代入代數式求出函數關系式,令利潤z=440,
求出x的值;
(3)根據廠商每月的制造成本不超過540萬元,以及成本價18元,得出銷售單價的取值范
圍,進而得出最大利潤.
解:(1)由表格中數據可得:y與x之間的函數關系式為:y=kx+b,
把(20,60),(25,50)代入得:
![]()
解得:![]()
故y與x之間的函數關系式為:y=﹣2x+100;
(2)設總利潤為z,由題意得,
z=y(x﹣18)
=(﹣2x+100)(x﹣18)
=﹣2x2+136x﹣1800;
當z=440時,
﹣2x2+136x﹣1800=440,
解得:x1=28,x2=40.
答:當銷售單價為28元或40元時,廠商每月獲得的利潤為440萬元;
(3)∵廠商每月的制造成本不超過540萬元,每件制造成本為18元,
∴每月的生產量為:小于等于![]() =30萬件,
=30萬件,
y=﹣2x+100≤30,
解得:x≥35,
∵z=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴圖象開口向下,對稱軸右側z隨x的增大而減小,
∴x=35時,z最大為:510萬元.
當銷售單價為35元時,廠商每月獲得的利潤最大,最大利潤為510萬元.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:初中數學 來源: 題型:
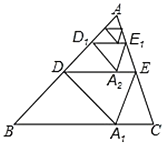
【題目】如圖,將![]() 沿著過
沿著過![]() 中點
中點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 邊上的
邊上的![]() 處,稱為第1次操作,折痕
處,稱為第1次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ,還原紙片后,再將
,還原紙片后,再將![]() 沿著過
沿著過![]() 中點
中點![]() 的直線折疊,使點
的直線折疊,使點![]() 落在
落在![]() 邊上的
邊上的![]() 處,稱為第2次操作,折痕
處,稱為第2次操作,折痕![]() 到
到![]() 的距離記為
的距離記為![]() ,按上述方法不斷操作下去…經過第2020次操作后得到的折痕
,按上述方法不斷操作下去…經過第2020次操作后得到的折痕![]() 到
到![]() 的距離記為
的距離記為![]() ,若
,若![]() ,則
,則![]() 的值為______.
的值為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“今有邑,東西七里,南北九里,各開中門,出東門一十五里有木,問:出南門幾何步而見木?”這段話摘自《九章算術》.意思是說:如圖,矩形城池ABCD,東邊城墻AB長9里,南邊城墻AD長7里,東門點E、南門點F分別是AB、AD中點,EG⊥AB,FH⊥AD,EG=15里,HG經過A點,則FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市計劃購進一批甲、乙兩種玩具,已知![]() 件甲種玩具的進價與
件甲種玩具的進價與![]() 件乙種玩具的進價的和為
件乙種玩具的進價的和為![]() 元,
元,![]() 件甲種玩具的進價與
件甲種玩具的進價與![]() 件乙種玩具的進價的和為
件乙種玩具的進價的和為![]() 元.
元.
(1)求每件甲種、乙種玩具的進價分別是多少元;
(2)如果購進甲種玩具有優惠,優惠方法是:購進甲種玩具超過![]() 件,超出部分可以享受
件,超出部分可以享受![]() 折優惠,若購進
折優惠,若購進![]()
![]() 件甲種玩具需要花費
件甲種玩具需要花費![]() 元,請你寫出
元,請你寫出![]() 與
與![]() 的函數表達式.
的函數表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究與發現:如圖1所示的圖形,像我們常見的學習用品--圓規.我們不妨把這樣圖形叫做“規形圖”,
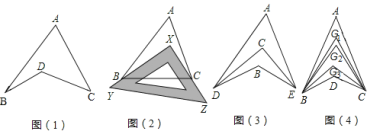
(1)觀察“規形圖”,試探究∠BDC與∠A、∠B、∠C之間的關系,并說明理由;
(2)請你直接利用以上結論,解決以下三個問題:
①如圖2,把一塊三角尺XYZ放置在△ABC上,使三角尺的兩條直角邊XY、XZ恰好經過點B、C,∠A=40°,則∠ABX+∠ACX等于多少度;
②如圖3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度數;
③如圖4,∠ABD,∠ACD的10等分線相交于點G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
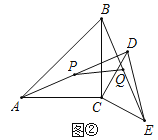
【題目】如圖1,![]() ,
,![]() ,
,![]() ,AD、BE相交于點M,連接CM.
,AD、BE相交于點M,連接CM.![]() 求證:
求證:![]() ;
;![]() 求
求![]() 的度數
的度數![]() 用含
用含![]() 的式子表示
的式子表示![]() ;
;![]() 如圖2,當
如圖2,當![]() 時,點P、Q分別為AD、BE的中點,分別連接CP、CQ、PQ,判斷
時,點P、Q分別為AD、BE的中點,分別連接CP、CQ、PQ,判斷![]() 的形狀,并加以證明.
的形狀,并加以證明.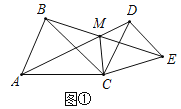
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,分別以Rt△ABC的直角邊AC及斜邊AB向外作等邊△ACD,等邊△ABE.已知∠BAC=30°,EF⊥AB,垂足為F,連接DF.
(1)試說明AC=EF;
(2)求證:四邊形ADFE是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個反比例函數![]() 和
和![]() 在第一象限內的圖象如圖所示,點P在
在第一象限內的圖象如圖所示,點P在![]() 的圖象上,PC⊥
的圖象上,PC⊥![]() 軸于點C,交
軸于點C,交![]() 的圖象于點A,PC⊥
的圖象于點A,PC⊥![]() 軸于點D,交
軸于點D,交![]() 的圖象于點B. 當點P在
的圖象于點B. 當點P在![]() 的圖象上運動時,以下結論:
的圖象上運動時,以下結論:
①![]()
②![]() 的值不會發生變化
的值不會發生變化
③PA與PB始終相等
④當點A是PC的中點時,點B一定是PD的中點.
其中一定不正確的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=2,BC=5,E、P分別在AD.BC上,且DE=BP=1.連接BE,EC,AP,DP,PD與CE交于點F,AP與BE交于點H.
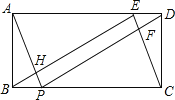
(1)判斷△BEC的形狀,并說明理由;
(2)判斷四邊形EFPH是什么特殊四邊形,并證明你的判斷;
(3)求四邊形EFPH的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com