
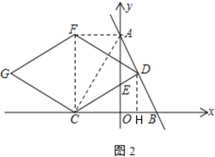
【題目】如圖1,直線![]() 分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
分別與y軸、x軸交于點A、點B,點C的坐標為(-3,0),D為直線AB上一動點,連接CD交y軸于點E.
(1) 點B的坐標為__________,不等式![]() 的解集為___________
的解集為___________
(2) 若S△COE=S△ADE,求點D的坐標;
(3) 如圖2,以CD為邊作菱形CDFG,且∠CDF=60°.當點D運動時,點G在一條定直線上運動,請求出這條定直線的解析式.


【答案】(1)(3,0)、x<3;(2)∴D(![]() );(3)
);(3)![]()
【解析】(1)用坐標軸上點的特點及不等式的解法求解即可;(2)設點D 的縱坐標
為![]() ,由S△COE=S△ADE可得S△AOB=S△CBD,求出
,由S△COE=S△ADE可得S△AOB=S△CBD,求出![]() ,進而求出
,進而求出![]() ;(3) 連接CF, AC由全等三角形的判定可得△CAF≌△CBD得到AF∥x軸,設出點D 的坐標結合直線
;(3) 連接CF, AC由全等三角形的判定可得△CAF≌△CBD得到AF∥x軸,設出點D 的坐標結合直線![]() 得到關于m的方程,進而求解.
得到關于m的方程,進而求解.
(1) (3,0)、x<3
(2) ∵S△COE=S△ADE
∴S△AOB=S△CBD
即![]() ,yD=
,yD=![]()
當y=![]() 時,
時,![]()
∴D(![]() )
)
(3) 連接CF
∵∠CDF=60°
∴△CDF為等邊三角形
連接AC
∵AB=AC=BC=6
∴△ABC為等邊三角形
∴△CAF≌△CBD(SAS)
∴∠CAF=∠ACB=60°
∴AF∥x軸
設D(m,![]() )
)
過點D作DH⊥x軸于H
∴BH=3-m,DB=6-2m=AF
∴F(2m-6,![]() )
)
由平移可知:G(m-9,![]() )
)
令![]()
∴點G在直線![]() 上.
上.


科目:初中數學 來源: 題型:
【題目】小明在學習過程中遇到這樣一個問題:
“一個木箱漂浮在河水中,隨河水向下游漂去,在木箱上游和木箱下游各有一條小船,分別為甲船和乙船,兩船距木箱距離相等,同時劃向木箱,若兩船在靜水中劃行的速度是30m/min,那么哪條小船先遇到木箱?”
小明是這樣分析解決的:
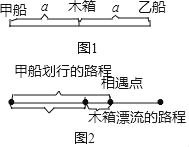
小明想通過比較甲乙兩船遇見木箱的時間,知道哪條小船先遇見木箱.設甲船遇見木箱的時間為xmin,乙船遇見木箱的時間為ymin,開始時兩船與木箱距離相等,都設為am,如圖1.
如圖2,利用甲船劃行的路程﹣木箱漂流的路程=開始時甲船與木箱的距離:
列方程:x(30+5)﹣5x=a
解得,x=![]()
所以甲船遇見木箱的時間為![]() min.
min.
(1)參照小明的解題思路繼續完成上述問題;
(2)借鑒小明解決問題的方法和(1)中發現的結論解決下面問題:
問題:“在一河流中甲乙兩條小船,同時從A地出發,甲船逆流而上,乙船順流而下;劃行10分鐘后,乙船發現船上木箱不知何時掉入水中,乙船立即通知甲船,兩船同時掉頭尋找木箱,若兩船在靜水中劃行的速度是v(單位:m/min,v大于5),水流速度是5m/min,兩船同時遇見木箱,那么木箱是出發幾分鐘后掉入水中的?”
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“陽光體育一小時”活動,根據學校實際情況,決定開設A:踢毽子;B:籃球:C:跳繩;D:乒乓球四種運動項目.為了解學生最喜歡哪一種運動項目,隨機抽取了一部分學生進行調查,并將調查結果繪制成如兩個統計圖.請結合圖中的信息解答下列問題:
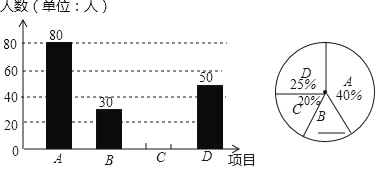
(1)本次共調查了多少名學生?
(2)請將兩個統計圖補充完整.
(3)求圖中“A”層次所在扇形的圓心角的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
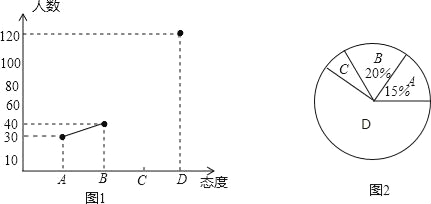
【題目】中學生帶手機上學的現象越來越受到社會的關注,為此某記者隨機調查了市區某校七年級若干名中學生家長對這種現象的態度(態度分為:A.無所謂;B.基本贊成;C.贊成;D.反對).統計員在將測試數據繪制成圖表時發現,反對漏統計6人,贊成漏統計4人,于是及時更正,從而形成如下圖表.請按正確數據解答下列各題:
家長對中學生帶手機上學各項態度人數統計表和統計圖:
態度 | 調整前人數 | 調整后人數 |
A.無所謂 | 30 | 30 |
B.基本贊成 | 40 | 40 |
C.贊成 | ||
D.反對 | 114 | 120 |
(1)此次抽樣調查中,共調查了多少名中學生家長;
(2)填寫統計表,并根據調整后數據補全折線統計圖;
(3)根據抽樣調查結果,請你估計該市城區6000名中學生家長中有多少名家長持反對態度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一果農販賣的西紅柿,其重量與價錢成一次函數關系.小華向果農買一竹籃的西紅柿,含竹籃稱得總重量為15公斤,付西紅柿的錢26元,若再加買0.5公斤的西紅柿,需多付1元,則空竹籃的重量為多少?( )
A. 1.5 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學計劃從一文體公司購買甲,乙兩種型號的小黑板,經洽談,購買一塊甲型小黑板比購買一塊乙型小黑板多用20元,且購買2塊甲型小黑板和3塊乙型小黑板共需440元.
(1)求購買一塊甲型小黑板、一塊乙型小黑板各需多少元?
(2)根據該中學實際情況,需從文體公司購買甲,乙兩種型號的小黑板共60塊,要求購買甲,乙兩種型號小黑板的總費用不超過5240元.并且購買甲型小黑板的數量不小于購買乙型小黑板數量的 ![]() .則該中學從文體公司購買甲,乙兩種型號的小黑板有哪幾種方案?哪種方案的總費用最低?
.則該中學從文體公司購買甲,乙兩種型號的小黑板有哪幾種方案?哪種方案的總費用最低?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星期天的早晨,小明騎自行車從家出發,到離家1050米的書店買書,出發1分鐘后,他到達離家150米的地方,又過1分鐘后,小明加快了速度.如圖所示是小明從家出發后離家的路程y(米)與他騎自行車的時間x(分鐘)之間的函數圖象.根據圖象解答下列問題: 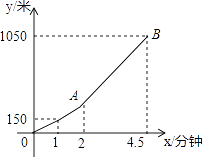
(1)直接寫出點A的坐標,并求線段AB所在的直線的函數解析式.
(2)求小明出發多長時間后,離書店還剩210米的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填空,完成下列說理過程
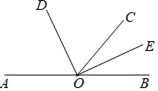
如圖,點A,O,B在同一條直線上,OD,OE分別平分∠AOC和∠BOC.求∠DOE的度數.
解:因為OD是∠AOC的平分線,
所以∠COD=![]() ∠AOC.
∠AOC.
因為OE是∠BOC 的平分線,
所以 =![]() ∠BOC.
∠BOC.
所以∠DOE=∠COD+∠COE=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com