
【題目】已知,![]() 是⊙O的直徑,弦
是⊙O的直徑,弦![]() 垂直平分
垂直平分![]() ,垂足為
,垂足為![]() ,連接
,連接![]() .
.
(1)如圖1,求![]() 的度數(shù);
的度數(shù);
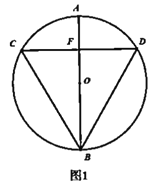
(2)如圖2,點(diǎn)![]() 分別為
分別為![]() 上一點(diǎn),并且
上一點(diǎn),并且![]() ,連接
,連接![]() ,交點(diǎn)為G,R為
,交點(diǎn)為G,R為![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() 與
與![]() 交于點(diǎn)H,
交于點(diǎn)H,![]() ,求證:
,求證:![]() ;
;
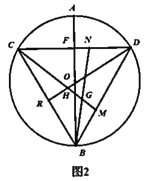
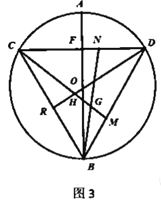
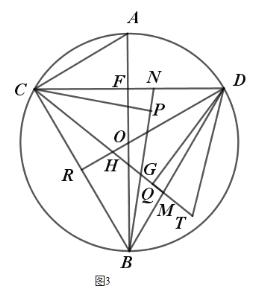
(3)如圖3,在(2)的條件下,![]() ,求⊙O半徑.
,求⊙O半徑.
【答案】(1)60°;
(2)證明見解析;
(3)半徑為![]() .
.
【解析】
(1)根據(jù)垂直平分線的性質(zhì)和圓的半徑相等可得出![]() 是等邊三角形,再根據(jù)同弧所對(duì)的圓周角相等即可求出答案;
是等邊三角形,再根據(jù)同弧所對(duì)的圓周角相等即可求出答案;
(2)![]() 垂直平分
垂直平分![]() ,
,![]() 是等邊三角形,得出△BCD是等邊三角形,得到BD=BC,∠CBM=∠BDN,再證明
是等邊三角形,得出△BCD是等邊三角形,得到BD=BC,∠CBM=∠BDN,再證明![]() ,根據(jù)外角設(shè)
,根據(jù)外角設(shè)![]() ,找到
,找到![]() 即可求出結(jié)論.
即可求出結(jié)論.
(3)在(2)的條件下,做輔助線:作CP⊥BN,DQ⊥CM,翻折DH到DT;求出![]() ,再根據(jù)角的關(guān)系得到∠DHT=∠CDT=∠T即
,再根據(jù)角的關(guān)系得到∠DHT=∠CDT=∠T即![]() ,由勾股定理求出DC即可求解半徑.
,由勾股定理求出DC即可求解半徑.
(1)證明:
連接![]()
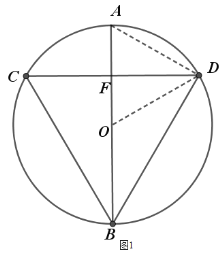
∵![]() 垂直平分
垂直平分![]() ,
,
又![]()
![]()
![]() 是等邊三角形
是等邊三角形
![]()
∵![]() ,
,
![]()
(2)證明:
∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,AB⊥CD,
,AB⊥CD,
∴∠ABC=∠ABD,BC=BD,
∵![]() 是等邊三角形,
是等邊三角形,
∴∠AOD=60°,
∴∠DBC=60°,
∴△BCD是等邊三角形,
∴BD=BC,∠CBM=∠BDN,
∵![]()
∴![]() ,
,
∴∠BCM=∠DBN,
∵∠DBN+∠CBN=60°,
∴∠BCM+∠CBN=60°,
∵∠BGM是△BGC的一個(gè)外角,
∴![]() ,
,
設(shè)![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵∠DHM是△DHC的一個(gè)外角,
∴![]() ,
,
∴![]() .
.
(3)如圖:連接AC,作CP⊥BN,DQ⊥CM,翻折DH到DT;
①在![]() 中:
中:
![]() ,
,![]() ,
,
勾股定理得![]() ,
,
②∵BC=CD,∠DCM=∠CBP,∠CPB=∠CQD=90°,
![]() ,
,
得![]() ,
,
翻折得![]() ,
,
∵![]() ,
,
∴∠DHT=∠DCM+∠CDR=60°-∠BCM+![]() =60°+
=60°+![]() ,
,
∴![]() ,
,
∵∠CDT=∠CDR+∠HDT
∴∠CDR+2(90°-∠DHT)=∠CDR+2(30°-∠BCM)=60°+![]() ,
,
∴∠DHT=∠CDT=∠T,
得![]()
③設(shè)![]() ,
,![]()
在![]() 中,
中,
![]() ,
,
![]() ,
,
得![]() ,
,
由(1)得∠ACF=30°,∠A=60°,
∴AC=![]() ,
,
∵![]() ,
,
∴AC=![]() ,
,
即半徑為![]() ;
;


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一個(gè)不透明的布袋里裝有4個(gè)標(biāo)有1,2,3,4的小球,它們的形狀、大小、質(zhì)地完全相同,小李從布袋里隨機(jī)取出一個(gè)小球,記下數(shù)字為x,小張?jiān)谑O碌?/span>3個(gè)小球中隨機(jī)取出一個(gè)小球,記下數(shù)字為y,這樣確定了點(diǎn)Q的坐標(biāo)(x,y).
(1)畫樹狀圖或列表,寫出點(diǎn)Q所有可能的坐標(biāo);
(2)求點(diǎn)Q(x,y)在函數(shù)y=﹣x+5圖象上的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
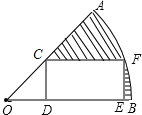
【題目】如圖,在半徑為![]() ,圓心角等于45°的扇形AOB內(nèi)部作一個(gè)矩形CDEF,使點(diǎn)C在OA上,點(diǎn)D、E在OB上,點(diǎn)F在弧AB上,且DE=2CD,則:
,圓心角等于45°的扇形AOB內(nèi)部作一個(gè)矩形CDEF,使點(diǎn)C在OA上,點(diǎn)D、E在OB上,點(diǎn)F在弧AB上,且DE=2CD,則:
(1)弧AB的長是(結(jié)果保留π)________;
(2)圖中陰影部分的面積為(結(jié)果保留π)________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】襄陽市精準(zhǔn)扶貧工作已進(jìn)入攻堅(jiān)階段.貧困戶張大爺在某單位的幫扶下,把一片坡地改造后種植了優(yōu)質(zhì)水果藍(lán)莓,今年正式上市銷售.在銷售的30天中,第一天賣出20千克,為了擴(kuò)大銷量,采取了降價(jià)措施,以后每天比前一天多賣出4千克.第x天的售價(jià)為y元/千克,y關(guān)于x的函數(shù)解析式為![]() 且第12天的售價(jià)為32元/千克,第26天的售價(jià)為25元/千克.已知種植銷售藍(lán)莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
且第12天的售價(jià)為32元/千克,第26天的售價(jià)為25元/千克.已知種植銷售藍(lán)莓的成木是18元/千克,每天的利潤是W元(利潤=銷售收入﹣成本).
(1)m= ,n= ;
(2)求銷售藍(lán)莓第幾天時(shí),當(dāng)天的利潤最大?最大利潤是多少?
(3)在銷售藍(lán)莓的30天中,當(dāng)天利潤不低于870元的共有多少天?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,![]() 的頂點(diǎn)
的頂點(diǎn)![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]()
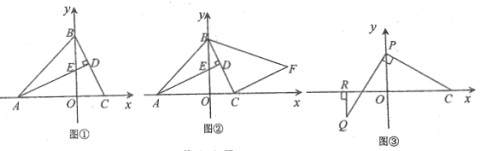
(1)如圖①,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)如圖②:將線段![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針旋轉(zhuǎn)
順時(shí)針旋轉(zhuǎn)![]() 后得線段
后得線段![]() ,連接
,連接![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)如圖③, 點(diǎn)![]() 為
為![]() 軸正半軸上一動(dòng)點(diǎn), 點(diǎn)
軸正半軸上一動(dòng)點(diǎn), 點(diǎn)![]() 在第二象限內(nèi),
在第二象限內(nèi),![]() 于
于![]() ,且
,且![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 垂直
垂直![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在8×6的方格紙ABCD中,AB=6,每個(gè)小方格紙的頂點(diǎn)為格點(diǎn),請(qǐng)按要求畫出格點(diǎn)多邊形,且所畫格點(diǎn)多邊形的頂點(diǎn)均不與點(diǎn)A,B,C,D重合.
(1)在圖1中畫一個(gè)格點(diǎn)三角形EFG,使得點(diǎn)E,F,G分別在AB,BC,AD上,且∠EFG=90°,
(2)在圖2中畫一個(gè)四邊形EFGH,使點(diǎn)F為邊BC的中點(diǎn),E,G,H分別落在邊AB,CD,DA上,且EG⊥FH,∠AEG≠90°.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
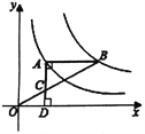
【題目】如圖,點(diǎn)![]() 在雙曲線
在雙曲線![]() 上,點(diǎn)
上,點(diǎn)![]() 在雙曲線
在雙曲線![]() 上,
上,![]() 軸,過點(diǎn)
軸,過點(diǎn)![]() 作
作![]() 軸于
軸于![]() ,連接
,連接![]() ,與
,與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,若
,若![]() ,則
,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】問題呈現(xiàn)
如圖1,在邊長為1的正方形網(wǎng)格中,連接格點(diǎn)![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,求
,求![]() 的值.
的值.
方法歸納
求一個(gè)銳角的三角函數(shù)值,我們往往需要找出(或構(gòu)造出)一個(gè)直角三角形.觀察發(fā)現(xiàn)問題中![]() 不在直角三角形中,我們常常利用網(wǎng)格畫平行線等方法解決此類問題.比如連接格點(diǎn)
不在直角三角形中,我們常常利用網(wǎng)格畫平行線等方法解決此類問題.比如連接格點(diǎn)![]() 、
、![]() ,可得
,可得![]() ,則
,則![]() ,連接
,連接![]() ,那么
,那么![]() 就變換到中
就變換到中![]() .
.
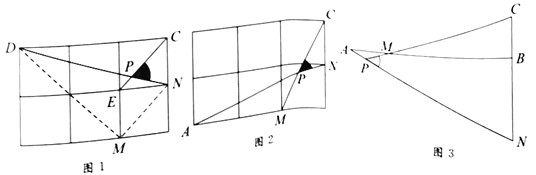
問題解決
(1)直接寫出圖1中![]() 的值為_________;
的值為_________;
(2)如圖2,在邊長為1的正方形網(wǎng)格中,![]() 與
與![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,求
,求![]() 的值;
的值;
思維拓展
(3)如圖3,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,且
上,且![]() ,延長
,延長![]() 到
到![]() ,使
,使![]() ,連接
,連接![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ,用上述方法構(gòu)造網(wǎng)格求
,用上述方法構(gòu)造網(wǎng)格求![]() 的度數(shù).
的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明從家去上學(xué),先步行一段路,因時(shí)間緊,他改騎共享單車,結(jié)果到學(xué)校時(shí)遲到了7min,其行駛的路程![]() (單位:
(單位:![]() )與時(shí)間
)與時(shí)間![]() (單位:
(單位:![]() )的關(guān)系如圖.若他出門時(shí)直接騎共享單車(兩次騎車速度相同),則下列說法正確的是( )
)的關(guān)系如圖.若他出門時(shí)直接騎共享單車(兩次騎車速度相同),則下列說法正確的是( )
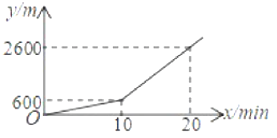
A.小明會(huì)遲到2min到校B.小明剛好按時(shí)到校
C.小明可以提前1min到校D.小明可以提前2min到校
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com