
【題目】已知一次函數y=﹣x+m的圖象與反比例函數![]() 的圖象交于A、B兩(點A在點B的左側),點P為x軸上一動點,當有且只有一個點P,使得∠APB=90°,則m的值為_____.
的圖象交于A、B兩(點A在點B的左側),點P為x軸上一動點,當有且只有一個點P,使得∠APB=90°,則m的值為_____.
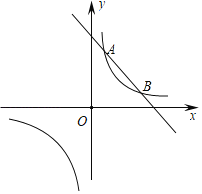
【答案】4
【解析】
根據題意以AB為直徑是圓與x軸相切于點P,根據直線的解析式即可證得△COD是等腰直角三角形,進而求得AB=m,根據平行線分線段成比例定理求得MC=BM=![]() m,即可求得B點的坐標,根據反比例函數圖象上點的坐標特征得出
m,即可求得B點的坐標,根據反比例函數圖象上點的坐標特征得出![]() m=2,解方程求得即可.
m=2,解方程求得即可.
設直線y=﹣x+m交x、y軸分別為C、D,
∴OD=OC=m,
∴△COD是等腰三角形,CD=![]() m,
m,
∴∠OCD=45°,
∵點P為x軸上一動點,有且只有一個點P,使得∠APB=90°,
∴以AB為直徑是圓與x軸相切于點P,
設AB的中點為I,
∴IP⊥x軸,IA=IC=![]() m,
m,
∵I是CD的中點,
∴IP=![]() OD=
OD=![]() m,
m,
∴IB=![]() m,
m,
∴BC=IC﹣IB=![]() m,
m,
∵BM∥IP,
∴![]() ,即
,即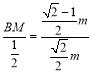
∴BM=![]() m
m
∵△BMC是等腰直角三角形,
∴MC=BM=![]() m,
m,
∴OM=m﹣![]() m=
m=![]() m,
m,
∴B(![]() ,
,![]() m),
m),
∵點B在反比例函數y=![]() 的圖象上,
的圖象上,
∴![]()
![]() m=2
m=2
解得m
故答案為4.


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(﹣1,0),與y軸的交點B在(0,﹣2)和(0,﹣1)之間(不包括這兩點),對稱軸為直線x=1.下列結論:①abc>0;②4a+2b+c>0;③![]() <a<
<a<![]() ;④b>c.其中含所有正確結論的選項是( )
;④b>c.其中含所有正確結論的選項是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的對角線交于點
的對角線交于點![]() .點
.點![]() 在
在![]() 邊上,
邊上,![]() 連結
連結![]() 交對角線
交對角線![]() 于點
于點![]() 是線段
是線段![]() 的中點,連結
的中點,連結![]() .
.
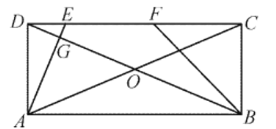
(1)求證:![]() .
.
(2)判斷![]() 與
與![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
(3)若![]() 和
和![]() 面積分別為
面積分別為![]() 和
和![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文化用品商店準備購進甲、乙兩種書包進行銷售,經調查,乙書包的單價比甲書包貴![]() 元,用
元,用![]() 元購進乙書包的個數與用
元購進乙書包的個數與用![]() 元購進甲書包的個數相等.
元購進甲書包的個數相等.
(1)求甲、乙兩種書包的進價分別為多少元?
(2)商戶購進甲、乙兩種書包共![]() 個進行試銷,其中甲書包的個數不少于
個進行試銷,其中甲書包的個數不少于![]() 個,且甲書包的個數 的
個,且甲書包的個數 的![]() 倍不大于乙書包的個數,已知甲書包的售價為
倍不大于乙書包的個數,已知甲書包的售價為![]() 元/個,乙書包的售價為
元/個,乙書包的售價為![]() 元/個,且 全部售出,設購進甲書包
元/個,且 全部售出,設購進甲書包![]() 個,求該商店銷售這批書包的利潤
個,求該商店銷售這批書包的利潤![]() 與
與![]() 之間的函數關系式,并 寫出
之間的函數關系式,并 寫出![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,該店將![]() 個書包全部售出后,使用所獲的利潤又購進
個書包全部售出后,使用所獲的利潤又購進![]() 個書包捐贈給 貧困地區兒童,這樣該商店這批書包共獲利
個書包捐贈給 貧困地區兒童,這樣該商店這批書包共獲利![]() 元.請求出該店第二次進貨所選用的進貨方案?
元.請求出該店第二次進貨所選用的進貨方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數y=x+3與x軸、y軸分別交于點A、B,將直線AB向下平移與反比例函數![]() (x>0)交于點C、D,連接BC交x軸于點E,連接AC,已知BE=3CE,且S△ACE=
(x>0)交于點C、D,連接BC交x軸于點E,連接AC,已知BE=3CE,且S△ACE=![]() .
.
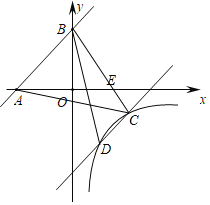
(1)求直線BC和反比例函數解析式;(2)連接BD,求△BCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 過點
過點![]() .
.
(1)若點![]() 也在該拋物線上,請用含
也在該拋物線上,請用含![]() 的關系式表示
的關系式表示![]() ;
;
(2)若該拋物線上任意不同兩點![]() 、
、![]() 都滿足:當
都滿足:當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;若以原點
;若以原點![]() 為圓心,
為圓心,![]() 為半徑的圓與拋物線的另兩個交點為
為半徑的圓與拋物線的另兩個交點為![]() 、
、![]() (點
(點![]() 在點
在點![]() 左側),且
左側),且![]() 有一個內角為
有一個內角為![]() ,求拋物線的解析式;
,求拋物線的解析式;
(3)在(2)的條件下,若點![]() 與點
與點![]() 關于點
關于點![]() 對稱,且
對稱,且![]() 、
、![]() 、
、![]() 三點共線,求證:
三點共線,求證:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,點M、N分別在線段AC、AB上,將△ANM沿直線MN折疊,使點A的對應點D恰好落在線段BC上,當△DCM為直角三角形時,折痕MN的長為__.
+4,點M、N分別在線段AC、AB上,將△ANM沿直線MN折疊,使點A的對應點D恰好落在線段BC上,當△DCM為直角三角形時,折痕MN的長為__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在以“青春心向覺,建功新時代”為主題的校園文化藝術節期間,舉辦了![]() 合唱,
合唱,![]() 群舞,
群舞,![]() 書法,
書法,![]() 演講共四個項目的比賽,要求每位學生必須參加且僅參加一項,小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中信息解答下列問題:
演講共四個項目的比賽,要求每位學生必須參加且僅參加一項,小紅隨機調查了部分學生的報名情況,并繪制了下列兩幅不完整的統計圖,請根據統計圖中信息解答下列問題:
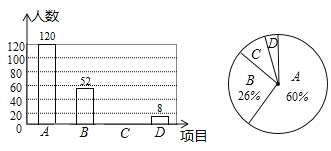
(1)本次調查的學生總人數是多少?扇形統計圖中“![]() ”部分的圓心角度數是多少?
”部分的圓心角度數是多少?
(2)請將條形統計圖補充完整;
(3)若全校共有1800名學生,請估計該校報名參加書法和演講比賽的學生共有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com