
【題目】超越公司將某品牌農副產品運往新時代市場進行銷售,記汽車行駛時為t小時,平均速度為v千米/小時(汽車行駛速度不超過100千米/小時).根據經驗,v,t的一組對應值如下表:
v(千米/小時) | 75 | 80 | 85 | 90 | 95 |
t(小時) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根據表中的數據,求出平均速度v(千米/小時)關于行駛時間t(小時)的函數表達式;
(2)汽車上午7:30從超越公司出發,能否在上午10:00之前到達新時代市場?請說明理由.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某工廠甲、乙兩名工人參加操作技能培訓.他們在培訓期間參加的8次測試成績記錄如下表:
甲 | 73 | 82 | 70 | 85 | 80 | 70 | 75 | 65 |
乙 | 85 | 72 | 78 | 71 | 83 | 69 | 74 | 68 |
則下列說法錯誤的是( )
A.甲、乙的平均成績都是75
B.甲成績的眾數是70
C.乙成績的中位數是73
D.若從中選派一人參加操作技能比賽,從成績穩定性考慮,應選甲
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在菱形ABCD中,對角線AC、BD交于點O,且AC=16cm,BD=12cm;點P從點A出發,沿AD方向勻速運動,速度為2cm/s;點Q從點C出發,沿CO方向勻速運動,速度為1cm/s;若P、Q兩點同時出發,當一個點停止運動時,另一個點也停止運動.過點Q作MQ∥BC,交BD于點M,設運動時間為t(s)(0<t<5).解答下列問題:
(1)求t為何值時,線段AQ、線段PM互相平分.
(2)設四邊形APQM的面積為Scm2 , 求S關于t的函數關系式;設菱形ABCD的面積為SABCD , 求是否存在一個時刻t,使S:SABCD=2:5?如果存在,求出t,如果不存在,請說明理由.
(3)求時刻t,使得以M、P、Q為頂點的三角形是直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,△ABC的角平分線BD、CE相交于點P.
(1)如果∠A=70°,求∠BPC的度數;
(2)如圖②,過P點作直線MN∥BC,分別交AB和AC于點M和N,試求∠MPB+∠NPC的度數(用含∠A的代數式表示);
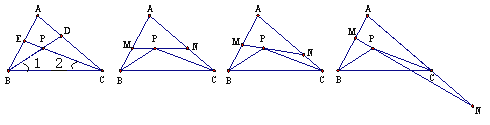
① ② ③ ④
在(2)的條件下,將直線MN繞點P旋轉.
(ⅰ)當直線MN與AB、AC的交點仍分別在線段AB和AC上時,如圖③,試探索∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由;
(ⅱ)當直線MN與AB的交點仍在線段AB上,而與AC的交點在AC的延長線上時,如圖④,試問(ⅰ)中∠MPB、∠NPC、∠A三者之間的數量關系是否仍然成立?若成立,請說明你的理由;若不成立,請給出∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,在△ABC中,∠C=60°,∠A=40°.

(1)用尺規作圖作AB的垂直平分線,交AC于點D,交AB于點E(保留作圖痕跡,不要求寫作法和證明);
(2)求證:BD平分∠CBA.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一張直角三角形紙片,兩直角邊長AC=6cm,BC=8cm,將△ABC折疊,使點B與點A重合,折痕為DE,則CD等于( )
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的袋子中裝有20個球,其中紅球6個,白球和黑球若干個,每個球除顏色外完全相同.
(1)小明通過大量重復試驗(每次將球攪勻后,任意摸出一個球,記下顏色后放回)發現,摸出的黑球的頻率在0.4附近擺動,請你估計袋中黑球的個數.
(2)若小明摸出的第一個球是白球,不放回,從袋中余下的球中再任意摸出一個球,摸出白球的概率是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com