
【題目】如圖,在四邊形ABCD中,AD∥BC, ![]() ,點E是BC的中點,連接AE、BD.若EA⊥AB,BC=26,DC=12,求△ABD的面積.
,點E是BC的中點,連接AE、BD.若EA⊥AB,BC=26,DC=12,求△ABD的面積.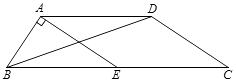
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為坐標原點,直線l1:y=![]() x與直線l2:y=﹣x+6交于點A,l2與x軸交于B,與y軸交于點C.
x與直線l2:y=﹣x+6交于點A,l2與x軸交于B,與y軸交于點C.
(1)求△OAC的面積;
(2)如點M在直線l2上,且使得△OAM的面積是△OAC面積的![]() ,求點M的坐標.
,求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題背景
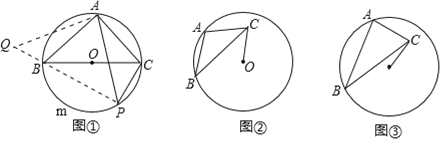
如圖①,BC是⊙O的直徑,點A在⊙O上,AB=AC,P為BmC上一動點(不與B,C重合),求證: ![]() PA=PB+PC.
PA=PB+PC.
小明同學觀察到圖中自點A出發有三條線段AB,AP,AC,且AB=AC,這就為旋轉作了鋪墊.于是,小明同學有如下思考過程:
第一步:將△PAC繞著點A順時針旋轉90°至△QAB(如圖①);
第二步:證明Q,B,P三點共線,進而原題得證.
請你根據小明同學的思考過程完成證明過程.
(2)類比遷移
如圖②,⊙O的半徑為3,點A,B在⊙O上,C為⊙O內一點,AB=AC,AB⊥AC,垂足為A,求OC的最小值.
(3)拓展延伸
如圖③,⊙O的半徑為3,點A,B在⊙O上,C為⊙O內一點,AB=![]() AC,AB⊥AC,垂足為A,則OC的最小值為 .
AC,AB⊥AC,垂足為A,則OC的最小值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題發現:
(![]() )如圖①,
)如圖①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上任意一點,則
邊上任意一點,則![]() 的最小值為__________.
的最小值為__________.
(![]() )如圖②,矩形
)如圖②,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、點
、點![]() 分別在
分別在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
(![]() )如圖③,矩形
)如圖③,矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊上一點,且
邊上一點,且![]() ,點
,點![]() 是
是![]() 邊上的任意一點,把
邊上的任意一點,把![]() 沿
沿![]() 翻折,點
翻折,點![]() 的對應點為點
的對應點為點![]() ,連接
,連接![]() 、
、![]() ,四邊形
,四邊形![]() 的面積是否存在最小值,若存在,求這個最小值及此時
的面積是否存在最小值,若存在,求這個最小值及此時![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com