
【題目】先仔細閱讀材料,再嘗試解決問題:我們在求代數式![]() 的最大或最小值時,通過利用公式
的最大或最小值時,通過利用公式![]() 對式子作如下變形:
對式子作如下變形:
![]() ,
,
因為![]() ,
,
所以![]() ,
,
因此![]() 有最小值2,
有最小值2,
所以,當![]() 時,
時,![]() ,
,![]() 的最小值為2.
的最小值為2.
同理,可以求出![]() 的最大值為7.
的最大值為7.
通過上面閱讀,解決下列問題:
(1)填空:代數式![]() 的最小值為______________;代數式
的最小值為______________;代數式![]() 的最大值為______________;
的最大值為______________;
(2)求代數式![]() 的最大或最小值,并寫出對應的
的最大或最小值,并寫出對應的![]() 的取值;
的取值;
(3)求代數式![]() 的最大或最小值,并寫出對應的
的最大或最小值,并寫出對應的![]() 、
、![]() 的值.
的值.
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分線交BC于E,連接DE.
(1)說明點D在△ABE的外接圓上;
(2)若∠AED=∠CED,試判斷直線CD與△ABE外接圓的位置關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,點E,F分別在AB,CD上,連接EF,∠AEF,∠CFE的平分線交于點G,∠BEF,∠DFE的平分線交于點H.易證∠EHF=∠EGF=∠GEH=90°,從而可知四邊形EGFH是矩形.
小明繼續進行了探索,過G作MN∥EF,分別交AB,CD于點M,N,過H作PQ∥EF,分別交AB,CD于點P,Q,得到四邊形MNQP,此時,他猜想四邊形MNQP是菱形,請在下列框中補全他的證明思路.
由AB∥CD,MN∥EF,PQ∥EF,易證四邊形MNQP是平行四邊形.要證平行四邊形MNQP是菱形,只要證MN=NQ.由已知條件_____,MN∥EF,可得NG=NF,故只要證GM=FQ,即證△MGE≌△QFH.易證_____,_____,故只要證∠MGE=∠QFH,易證∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得證.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(﹣4,a),B(﹣1,2)是一次函數y1=kx+b與反比例函數y2=![]() (m<0)圖象的兩個交點,AC⊥x軸于C.
(m<0)圖象的兩個交點,AC⊥x軸于C.

(1)求出k,b及m的值.
(2)根據圖象直接回答:在第二象限內,當y1>y2時,x的取值范圍是 ________.
(3)若P是線段AB上的一點,連接PC,若△PCA的面積等于![]() ,求點P坐標.
,求點P坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,正方形頂點![]() 為
為![]() 軸正半軸上一點,點
軸正半軸上一點,點![]() 在第一象限,點
在第一象限,點![]() 的坐標為
的坐標為![]() ,連接
,連接![]() .動點
.動點![]() 在射線
在射線![]() 上(點
上(點![]() 不與點
不與點![]() 、點
、點![]() 重合),點
重合),點![]() 在線段
在線段![]() 的延長線上,連接
的延長線上,連接![]() 、
、![]() ,
,![]() ,設
,設![]() 的長為
的長為![]() .
.

(1)填空:線段![]() 的長=________,線段
的長=________,線段![]() 的長=________;
的長=________;
(2)求![]() 的長,并用含
的長,并用含![]() 的代數式表示.
的代數式表示.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形一個角的平分線分矩形一邊為2cm和3cm兩部分,則這個矩形的面積為( )
A.10cm2B.15cm2C.12cm2D.10cm2或15cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位欲從內部招聘管理人員一名,對甲、乙、丙三名候選人進行了筆試和面試兩項測試,三人的測試成績如下表所示:
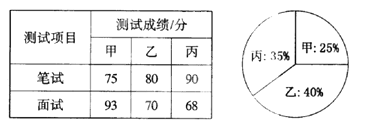
根據錄用程序,組織200名職工對三人利用投票推薦的方式進行民主評議,三人得票率(沒有棄權票,每位職工只能推薦1人)如扇形圖所示,每得一票記作1分.
(l)如果根據三項測試的平均成績確定錄用人選,那么誰將被錄用(精確到 0.01 )?
(2)根據實際需要,單位將筆試、面試、民主評議三項測試得分按5 : 2 : 3的比例確定個人成績,那么誰將被錄用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】投資1萬元圍一個矩形菜園(如圖),其中一邊靠墻,另外三邊選用不同材料建造.墻長24 m,平行于墻的邊的費用為200元/m,垂直于墻的邊的費用為150元/m,設平行于墻的邊長為x m.
(1)設垂直于墻的一邊長為y m,直接寫出y與x之間的函數關系式;
(2)若菜園面積為384 m2,求x的值;
(3)求菜園的最大面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
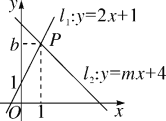
【題目】如圖,直線l1:y=2x+1與直線l2:y=mx+4相交于點P(1,b).
(1)求b,m的值;
(2)垂直于x軸的直線與直線l1,l2,分別交于點C,D,垂足為點E,設點E的坐標為(a,0)若線段CD長為2,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com