
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:![]() (p,q是正整數,且
(p,q是正整數,且![]() ),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的完美分解.并規定:
),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的完美分解.并規定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因為18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一個兩位正整數t,其個位數字是a,十位數字為![]() ,交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為36,那么我們稱這個數為“和諧數”,求所有“和諧數”;
,交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為36,那么我們稱這個數為“和諧數”,求所有“和諧數”;
(3)在(2)所得“和諧數”中,求F(t)的最大值.
 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】將正整數1,2,3,4,5,……排列成如圖所示的數陣:
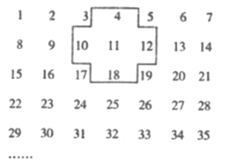
(1)十字框中五個數的和與框正中心的數11有什么關系?
(2)若將十字框上下、左右平移,可框住另外五個數,這五個數的和與框正中心的數還有這種規律嗎?請說明理由;
(3)十字框中五個數的和能等于180嗎?若能,請寫出這五個數;若不能,請說明理由;
(4)十字框中五個數的和能等于2020嗎?若能,請寫出這五個數;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣教育局為了豐富初中學生的大課間活動,要求各學校開展形式多樣的陽光體育活動.某中學就“學生體育活動興趣愛好”的問題,隨機調查了本校某班的學生,并根據調查結果繪制成如下的不完整的扇形統計圖和條形統計圖:

(1)在這次調查中,喜歡籃球項目的同學有 人,在扇形統計圖中,“乒乓球”的百分比為 %,如果學校有800名學生,估計全校學生中有 人喜歡籃球項目.
(2)請將條形統計圖補充完整.
(3)在被調查的學生中,喜歡籃球的有2名女同學,其余為男同學.現要從中隨機抽取2名同學代表班級參加校籃球隊,請直接寫出所抽取的2名同學恰好是1名女同學和1名男同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
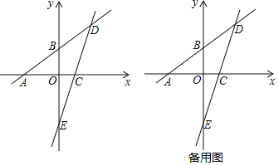
【題目】已知:如圖,一次函數y=![]() x+3的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.
x+3的圖象分別與x軸、y軸相交于點A、B,且與經過點C(2,0)的一次函數y=kx+b的圖象相交于點D,點D的橫坐標為4,直線CD與y軸相交于點E.
(1)直線CD的函數表達式為______;(直接寫出結果)
(2)在x軸上求一點P使△PAD為等腰三角形,直接寫出所有滿足條件的點P的坐標.
(3)若點Q為線段DE上的一個動點,連接BQ.點Q是否存在某個位置,將△BQD沿著直線BQ翻折,使得點D恰好落在直線AB下方的y軸上?若存在,求點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
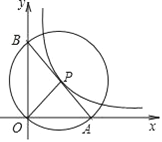
【題目】如圖,在平面直角坐標系中,O 為坐標原點,P是反比例函數![]() 圖象上任意一點,以P為圓心,PO為半徑的圓與x軸交于點 A、與y軸交于點B,連接AB.
圖象上任意一點,以P為圓心,PO為半徑的圓與x軸交于點 A、與y軸交于點B,連接AB.
(1)求證:P為線段AB的中點;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若拋物線L:y=ax2+bx+c(a,b,c是常數,abc≠0)與直線l都經過y軸上的同一點,且拋物線L的頂點在直線l上,則稱次拋物線L與直線l具有“一帶一路”關系,并且將直線l叫做拋物線L的“路線”,拋物線L叫做直線l的“帶線”.
(1)若“路線”l的表達式為y=2x﹣4,它的“帶線”L的頂點的橫坐標為﹣1,求“帶線”L的表達式;
(2)如果拋物線y=mx2﹣2mx+m﹣1與直線y=nx+1具有“一帶一路”關系,求m,n的值;
(3)設(2)中的“帶線”L與它的“路線”l在y軸上的交點為A.已知點P為“帶線”L上的點,當以點P為圓心的圓與“路線”l相切于點A時,求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
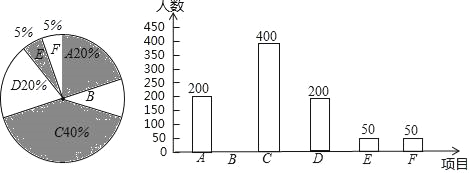
【題目】電視熱播節目“最強大腦”激發了學生的思考興趣,為滿足學生的需求,某學校抽取部分學生舉行“最強大腦”選拔賽,針對競賽成績分成以下六個等級A:0~50分;B:51~60分;C:61~70分;D:71~80分;E:81~90分;F:91~100分,根據調查結果繪制了如下尚不完整的統計圖,請你根據統計圖解答下列問題:
(1)此次競賽抽取的總人數為 ,請補全條形統計圖;
(2)若全市約有3萬名在校學生,試估計全市學生中競賽成績在71~90分的人數約有多少?
(3)若在此次接受調查的學生中,隨機抽查一人,則此人的成績在80分以上的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展“校園獻愛心”活動.準備向西部山區學校捐贈男、女兩種款式的書包,已知男款書包單價![]() 元/個,女款書包單價
元/個,女款書包單價![]() 元/個.
元/個.
![]() 原計劃募捐
原計劃募捐![]() 元,恰好可購買兩種款式的書包
元,恰好可購買兩種款式的書包![]() 個,問兩種款式的書包各買多少個?
個,問兩種款式的書包各買多少個?
![]() 在捐款活動中,師生積極性高,實際捐款額和書包數量都高于原計劃.快遞公司將這些書包裝箱運送,其中每箱書包數量相同.第一次他們領走這批的
在捐款活動中,師生積極性高,實際捐款額和書包數量都高于原計劃.快遞公司將這些書包裝箱運送,其中每箱書包數量相同.第一次他們領走這批的![]() ,結果裝了
,結果裝了![]() 箱還多
箱還多![]() 個書包;第二次他們把余下的
個書包;第二次他們把余下的![]() 領走.連同第一次裝箱剩下的
領走.連同第一次裝箱剩下的![]() 個書包一起,剛好裝了
個書包一起,剛好裝了![]() 箱.問:實際購買書包共多少個?
箱.問:實際購買書包共多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在紙面上有一數軸(如圖),折疊紙面.例如:若數軸上數2表示的點與數-2表示的點重合,則數軸上數-4,表示的點與數4表示的點重合,根據你對例題的理解,解答下列問題:
![]()
若數軸上數-3表示的點與數1表示的點重合.(請依據此情境解決下列問題)
①則數軸上數3表示的點與數 表示的點重合.
②若點![]() 到與原點的距離是5個單位長度,并且
到與原點的距離是5個單位長度,并且![]() ,
,![]() 兩點經折疊后重合,則點
兩點經折疊后重合,則點![]() 點表示的數是 .
點表示的數是 .
③若數軸上![]() ,
,![]() 兩點之間的距離為2018,并且
兩點之間的距離為2018,并且![]() ,
,![]() 兩點經折疊后重合,如果
兩點經折疊后重合,如果![]() 點表示的數比
點表示的數比![]() 點表示的數大,則
點表示的數大,則![]() 點表示的數是 ,則
點表示的數是 ,則![]() 點表示的數是 .
點表示的數是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com