
【題目】【探索發(fā)現(xiàn)】
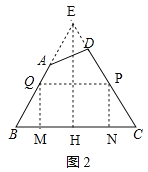
如圖①,是一張直角三角形紙片,∠B=60°,小明想從中剪出一個(gè)以∠B為內(nèi)角且面積最大的矩形,經(jīng)過多次操作發(fā)現(xiàn),當(dāng)沿著中位線DE、EF剪下時(shí),所得的矩形的面積最大,隨后,他通過證明驗(yàn)證了其正確性,并得出:矩形的最大面積與原三角形面積的比值為 .
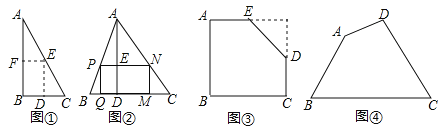
【拓展應(yīng)用】
如圖②,在△ABC中,BC=a,BC邊上的高AD=h,矩形PQMN的頂點(diǎn)P、N分別在邊AB、AC上,頂點(diǎn)Q、M在邊BC上,則矩形PQMN面積的最大值為 .(用含a,h的代數(shù)式表示)
【靈活應(yīng)用】
如圖③,有一塊“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明從中剪出了一個(gè)面積最大的矩形(∠B為所剪出矩形的內(nèi)角),求該矩形的面積.
【實(shí)際應(yīng)用】
如圖④,現(xiàn)有一塊四邊形的木板余料ABCD,經(jīng)測量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐師傅從這塊余料中裁出了頂點(diǎn)M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
,木匠徐師傅從這塊余料中裁出了頂點(diǎn)M、N在邊BC上且面積最大的矩形PQMN,求該矩形的面積.
【答案】【探索發(fā)現(xiàn)】![]() ;【拓展應(yīng)用】
;【拓展應(yīng)用】![]() ;【靈活應(yīng)用】720;【實(shí)際應(yīng)用】1944.
;【靈活應(yīng)用】720;【實(shí)際應(yīng)用】1944.
【解析】
試題分析:【探索發(fā)現(xiàn)】:由中位線知EF=![]() BC、ED=
BC、ED=![]() AB、由
AB、由![]() =
=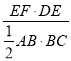 可得;
可得;
【拓展應(yīng)用】:由△APN∽△ABC知![]() ,可得PN=a﹣
,可得PN=a﹣![]() PQ,設(shè)PQ=x,由S矩形PQMN=PQPN═
PQ,設(shè)PQ=x,由S矩形PQMN=PQPN═![]() ,據(jù)此可得;
,據(jù)此可得;
【靈活應(yīng)用】:添加如圖1輔助線,取BF中點(diǎn)I,F(xiàn)G的中點(diǎn)K,由矩形性質(zhì)知AE=EH20、CD=DH=16,分別證△AEF≌△HED、△CDG≌△HDE得AF=DH=16、CG=HE=20,從而判斷出中位線IK的兩端點(diǎn)在線段AB和DE上,利用【探索發(fā)現(xiàn)】結(jié)論解答即可;
【實(shí)際應(yīng)用】:延長BA、CD交于點(diǎn)E,過點(diǎn)E作EH⊥BC于點(diǎn)H,由tanB=tanC知EB=EC、BH=CH=54,EH=![]() BH=72,繼而求得BE=CE=90,可判斷中位線PQ的兩端點(diǎn)在線段AB、CD上,利用【拓展應(yīng)用】結(jié)論解答可得.
BH=72,繼而求得BE=CE=90,可判斷中位線PQ的兩端點(diǎn)在線段AB、CD上,利用【拓展應(yīng)用】結(jié)論解答可得.
試題解析:【探索發(fā)現(xiàn)】
∵EF、ED為△ABC中位線,∴ED∥AB,EF∥BC,EF=![]() BC,ED=
BC,ED=![]() AB,又∠B=90°,∴四邊形FEDB是矩形,則
AB,又∠B=90°,∴四邊形FEDB是矩形,則![]() =
=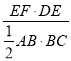 =
=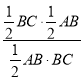 =
=![]() ,故答案為:
,故答案為:![]() ;
;
【拓展應(yīng)用】
∵PN∥BC,∴△APN∽△ABC,∴![]() ,即
,即![]() ,∴PN=a﹣
,∴PN=a﹣![]() PQ,設(shè)PQ=x,則S矩形PQMN=PQPN=x(a﹣
PQ,設(shè)PQ=x,則S矩形PQMN=PQPN=x(a﹣![]() x)=
x)=![]() =
=![]() ,∴當(dāng)PQ=
,∴當(dāng)PQ=![]() 時(shí),S矩形PQMN最大值為
時(shí),S矩形PQMN最大值為![]() ,故答案為:
,故答案為:![]() ;
;
【靈活應(yīng)用】
如圖1,延長BA、DE交于點(diǎn)F,延長BC、ED交于點(diǎn)G,延長AE、CD交于點(diǎn)H,取BF中點(diǎn)I,F(xiàn)G的中點(diǎn)K,
由題意知四邊形ABCH是矩形,∵AB=32,BC=40,AE=20,CD=16,∴EH=20、DH=16,∴AE=EH、CD=DH,在△AEF和△HED中,∵∠FAE=∠DHE,AE=AH,∠AEF=∠HED,∴△AEF≌△HED(ASA),∴AF=DH=16,同理△CDG≌△HDE,∴CG=HE=20,∴BI=![]() (AB+AF)=24,∵BI=24<32,∴中位線IK的兩端點(diǎn)在線段AB和DE上,過點(diǎn)K作KL⊥BC于點(diǎn)L,由【探索發(fā)現(xiàn)】知矩形的最大面積為
(AB+AF)=24,∵BI=24<32,∴中位線IK的兩端點(diǎn)在線段AB和DE上,過點(diǎn)K作KL⊥BC于點(diǎn)L,由【探索發(fā)現(xiàn)】知矩形的最大面積為![]() ×BGBF=
×BGBF=![]() ×(40+20)×(32+16)=720,答:該矩形的面積為720;
×(40+20)×(32+16)=720,答:該矩形的面積為720;
【實(shí)際應(yīng)用】
如圖2,延長BA、CD交于點(diǎn)E,過點(diǎn)E作EH⊥BC于點(diǎn)H,∵tanB=tanC=![]() ,∴∠B=∠C,∴EB=EC,∵BC=108cm,且EH⊥BC,∴BH=CH=
,∴∠B=∠C,∴EB=EC,∵BC=108cm,且EH⊥BC,∴BH=CH=![]() BC=54cm,∵tanB=
BC=54cm,∵tanB=![]() =
=![]() ,∴EH=
,∴EH=![]() BH=
BH=![]() ×54=72cm,在Rt△BHE中,BE=
×54=72cm,在Rt△BHE中,BE=![]() =90cm,∵AB=50cm,∴AE=40cm,∴BE的中點(diǎn)Q在線段AB上,∵CD=60cm,∴ED=30cm,∴CE的中點(diǎn)P在線段CD上,∴中位線PQ的兩端點(diǎn)在線段AB、CD上,由【拓展應(yīng)用】知,矩形PQMN的最大面積為
=90cm,∵AB=50cm,∴AE=40cm,∴BE的中點(diǎn)Q在線段AB上,∵CD=60cm,∴ED=30cm,∴CE的中點(diǎn)P在線段CD上,∴中位線PQ的兩端點(diǎn)在線段AB、CD上,由【拓展應(yīng)用】知,矩形PQMN的最大面積為![]() BCEH=1944cm2.
BCEH=1944cm2.
答:該矩形的面積為1944cm2.


 名校聯(lián)盟快樂課堂系列答案
名校聯(lián)盟快樂課堂系列答案 黃岡創(chuàng)優(yōu)卷系列答案
黃岡創(chuàng)優(yōu)卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知在長方形ABCD中, AD=8, AB=4,將長方形ABCD沿著對角線BD折疊,使點(diǎn)C落在 ![]() 處,
處, ![]() 交AD于點(diǎn)E.
交AD于點(diǎn)E.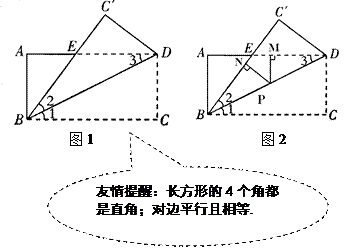
(1)求證:△BED是等腰三角形.
(2)求DE的長.
(3)如圖2,若點(diǎn)P是BD上一動點(diǎn), ![]() 于點(diǎn)N,
于點(diǎn)N, ![]() 于點(diǎn)M,問: PN+PM的長是否為定值?如果是,請求出該值,如果不是,請說明理由.
于點(diǎn)M,問: PN+PM的長是否為定值?如果是,請求出該值,如果不是,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某籃球隊(duì)12名隊(duì)員的年齡如下表所示:
年齡(歲) | 18 | 19 | 20 | 21 |
人數(shù) | 5 | 4 | 1 | 2 |
則這12名隊(duì)員年齡的眾數(shù)和中位數(shù)分別是( )
A.18,19B.18,19.5C.5,4D.5, 4.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,現(xiàn)有一張邊長為4的正方形紙片ABCD,點(diǎn)P為正方形AD邊上的一點(diǎn)(不與點(diǎn)A、點(diǎn)D重合)將正方形紙片折疊,使點(diǎn)B落在P處,點(diǎn)C落在G處,PG交DC于H,折痕為EF,連接BP、BH.(友情提醒:正方形的四條邊都相等,即AB=BC=CD=DA;四個(gè)內(nèi)角都是90°,即∠A=∠B=∠C=∠D=90°)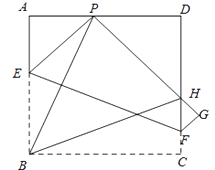
(1)求證:∠APB=∠BPH;
(2)當(dāng)點(diǎn)P在邊AD上移動時(shí),△PDH的周長是否發(fā)生變化?并證明你的結(jié)論;
(3)設(shè)AP為x,求出BE的長.(用含x的代數(shù)式表式)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于點(diǎn)E,H為BC上一點(diǎn),且BH=BA交AC于點(diǎn)F,連接FH.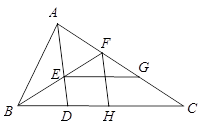
(1)求證:AE=FH;
(2)作EG//BC交AC于點(diǎn)G若AG=5,AC=8,求FG的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若2x3﹣ax2﹣5x+5=(2x2+ax﹣1)(x﹣b)+3,其中a,b為整數(shù),則ab的值為( )
A.2B.﹣2C.4D.﹣4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=1cm,AD=3cm,點(diǎn)Q從A點(diǎn)出發(fā),以1cm/s的速度沿AD向終點(diǎn)D運(yùn)動,點(diǎn)P從點(diǎn)C出發(fā),以1cm/s的速度沿CB向終點(diǎn)B運(yùn)動,當(dāng)這兩點(diǎn)中有一點(diǎn)到達(dá)自己的終點(diǎn)時(shí),另一點(diǎn)也停止運(yùn)動,兩點(diǎn)同時(shí)出發(fā),運(yùn)動了t秒.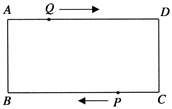
(1)當(dāng)0<t<3,判斷四邊形BQDP的形狀,并說明理由;
(2)求四邊形BQDP的面積S與運(yùn)動時(shí)間t的函數(shù)關(guān)系式;
(3)求當(dāng)t為何值時(shí),四邊形BQDP為菱形.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com