
【題目】下列條件:①∠A=∠B=∠C;②∠A∶∠B∶∠C=1∶2∶3;③∠A=90°+∠B;④∠A=∠B=![]() ∠C,能確定△ABC是直角三角形的條件有( )
∠C,能確定△ABC是直角三角形的條件有( )
A. 1個 B. 2個 C. 3個 D. 4個
【答案】B
【解析】①因為∠A=∠B=∠C,所以△ABC是等邊三角形,不是直角三角形,故不符合題意;
②因為∠A:∠B:∠C=1:2:3,設∠A=x,則x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形,符合題意;
③因為∠A=90°+∠B,∠A+∠B+∠C=180°,所以2∠B+∠C=90°,則∠A、∠B、∠C都不可能是90°,所以△ABC不是直角三角形,不符合題意;
④因為∠A=∠B=![]() ∠C,設∠A=x,則∠B=x,∠C=2x,由三角形內角和定理得,x+x+2x=180°,x=45°,∠C=2x=90°,所以△ABC是直角三角形,符合題意,
∠C,設∠A=x,則∠B=x,∠C=2x,由三角形內角和定理得,x+x+2x=180°,x=45°,∠C=2x=90°,所以△ABC是直角三角形,符合題意,
所以能確定△ABC是直角三角形的有②④共2個,
故選B.


科目:初中數學 來源: 題型:
【題目】如圖,點O是直線AB上任一點,射線OD和射線OE分別平分∠AOC和∠BOC.

(1)填空:與∠AOE互補的角是 ;
(2)若∠AOD=36°,求∠DOE的度數;
(3)當∠AOD=x°時,請直接寫出∠DOE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一架梯子長25米,斜靠在一面墻上,梯子底端離墻7米。
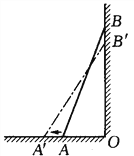
(1)這個梯子的頂端離地面有多高?
(2)如果梯子的頂端下滑了4米,那么梯子的底端在水平方向滑動了幾米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BAC=∠DAF=90°,AB=AC,AD=AF,點D、E為BC邊上的兩點,且∠DAE=45°,連接EF、BF,則下列結論:①△AED≌△AEF ②△AED為等腰三角形
③BE+DC>DE④BE2+DC2=DE2,其中正確的有( )個
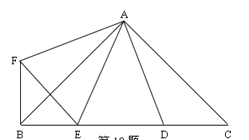
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=AC,∠BAC=120°,AB的垂直平分線交BC于點D,那么∠DAC的度數為( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一列數,第一個數為x1=1,第二個數為x2=3,從第三個數開始依次為x3,x4,…,xn,….從第二個數開始,每個數是左右相鄰兩個數和的一半,如x2=![]() ,x3=
,x3=![]() .
.
(1)求x3,x4,x5的值,并寫出計算過程;
(2)根據(1)的結果,推測x9等于多少;
(3)探索這一列數的規律,猜想第k(k為正整數)個數xk等于多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一外地游客到某特產專營店,準備購買精加工的豆腐乳和獼猴桃果汁兩種盒裝特產,若購買3盒豆腐乳和2盒獼猴桃果汁共需60元;購買1盒豆腐乳和3盒獼猴桃果汁共需55元.
(1)請分別求出每盒豆腐乳和每盒獼猴桃果汁的價格;
(2)該游客購買了4盒豆腐乳和2盒獼猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線BC與半徑為6的⊙O相切于點B,點M是圓上的動點,過點M作MC⊥BC,垂足為C,MC與⊙O交于點D,AB為⊙O的直徑,連接MA、MB,設MC的長為x,(6<x<12).
(1)當x=9時,求BM的長和△ABM的面積;
(2)是否存在點M,使MDDC=20?若存在,請求出x的值;若不存在,請說明理由.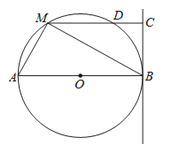
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com