
【題目】如圖1,二次函數(shù)y=﹣x2+bx+c的圖象過(guò)點(diǎn)A(3,0),B(0,4)兩點(diǎn),動(dòng)點(diǎn)P從A出發(fā),在線(xiàn)段AB上沿A→B的方向以每秒2個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng),過(guò)點(diǎn)P作PD⊥y于點(diǎn)D,交拋物線(xiàn)于點(diǎn)C.設(shè)運(yùn)動(dòng)時(shí)間為t(秒).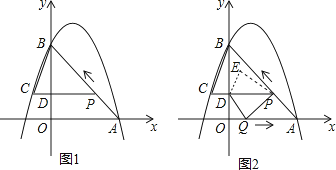
(1)求二次函數(shù)y=﹣x2+bx+c的表達(dá)式;
(2)連接BC,當(dāng)t= ![]() 時(shí),求△BCP的面積;
時(shí),求△BCP的面積;
(3)如圖2,動(dòng)點(diǎn)P從A出發(fā)時(shí),動(dòng)點(diǎn)Q同時(shí)從O出發(fā),在線(xiàn)段OA上沿O→A的方向以1個(gè)單位長(zhǎng)度的速度運(yùn)動(dòng).當(dāng)點(diǎn)P與B重合時(shí),P、Q兩點(diǎn)同時(shí)停止運(yùn)動(dòng),連接DQ,PQ,將△DPQ沿直線(xiàn)PC折疊得到△DPE.在運(yùn)動(dòng)過(guò)程中,設(shè)△DPE和△OAB重合部分的面積為S,直接寫(xiě)出S與t的函數(shù)關(guān)系及t的取值范圍.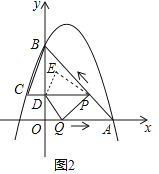
【答案】
(1)
解:把A(3,0),B(0,4)代入y=﹣x2+bx+c中得:
![]() 解得
解得 ![]() ,
,
∴二次函數(shù)y=﹣x2+bx+c的表達(dá)式為:y=﹣x2+ ![]() x+4
x+4
(2)
解:如圖1,
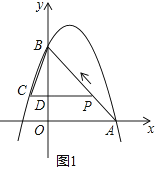
當(dāng)t= ![]() 時(shí),AP=2t,
時(shí),AP=2t,
∵PC∥x軸,
∴ ![]() ,
,
∴ ![]() ,
,
∴OD= ![]() =
= ![]() ×
× ![]() =
= ![]() ,
,
當(dāng)y= ![]() 時(shí),
時(shí), ![]() =﹣x2+
=﹣x2+ ![]() x+4,
x+4,
3x2﹣5x﹣8=0,
x1=﹣1,x2= ![]() ,
,
∴C(﹣1, ![]() ),
),
由 ![]() 得
得 ![]() ,
,
則PD=2,
∴S△BCP= ![]() ×PC×BD=
×PC×BD= ![]() ×3×
×3× ![]() =4
=4
(3)
解:如圖3,

當(dāng)點(diǎn)E在AB上時(shí),
由(2)得OD=QM=ME= ![]() ,
,
∴EQ= ![]() ,
,
由折疊得:EQ⊥PD,則EQ∥y軸
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
同理得:PD=3﹣ ![]() ,
,
∴當(dāng)0≤t≤ ![]() 時(shí),S=S△PDQ=
時(shí),S=S△PDQ= ![]() ×PD×MQ=
×PD×MQ= ![]() ×(3﹣
×(3﹣ ![]() )×
)× ![]() ,
,
S=﹣ ![]() t2+
t2+ ![]() t;
t;
當(dāng) ![]() <t≤2.5時(shí),
<t≤2.5時(shí),
如圖4,
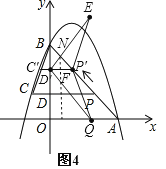
P′D′=3﹣ ![]() ,
,
點(diǎn)Q與點(diǎn)E關(guān)于直線(xiàn)P′C′對(duì)稱(chēng),則Q(t,0)、E(t, ![]() ),
),
∵AB的解析式為:y=﹣ ![]() x+4,
x+4,
D′E的解析式為:y= ![]() x+
x+ ![]() t,
t,
則交點(diǎn)N( ![]() ,
, ![]() ),
),
∴S=S△P′D′N= ![]() ×P′D′×FN=
×P′D′×FN= ![]() ×(3﹣
×(3﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() ),
),
∴S= ![]() t2﹣
t2﹣ ![]() t+
t+ ![]() .
.
【解析】(1)直接將A、B兩點(diǎn)的坐標(biāo)代入列方程組解出即可;(2)如圖1,要想求△BCP的面積,必須求對(duì)應(yīng)的底和高,即PC和BD;先求OD,再求BD,PC是利用點(diǎn)P和點(diǎn)C的橫坐標(biāo)求出,要注意符號(hào);(3)分兩種情況討論:①△DPE完全在△OAB中時(shí),即當(dāng)0≤t≤ ![]() 時(shí),如圖2所示,重合部分的面積為S就是△DPE的面積;②△DPE有一部分在△OAB中時(shí),當(dāng)
時(shí),如圖2所示,重合部分的面積為S就是△DPE的面積;②△DPE有一部分在△OAB中時(shí),當(dāng) ![]() <t≤2.5時(shí),如圖4所示,△PDN就是重合部分的面積S.本題是二次函數(shù)的綜合題,考查了利用待定系數(shù)法求二次函數(shù)和一次函數(shù)的解析式,并能利用方程組求出兩圖象的交點(diǎn),把方程和函數(shù)有機(jī)地結(jié)合在一起,使函數(shù)問(wèn)題簡(jiǎn)單化;同時(shí)考查了分類(lèi)討論的思想,這一思想在二次函數(shù)中經(jīng)常運(yùn)用,要熟練掌握;本題還與相似結(jié)合,利用相似三角形對(duì)應(yīng)邊的比來(lái)表示線(xiàn)段的長(zhǎng).
<t≤2.5時(shí),如圖4所示,△PDN就是重合部分的面積S.本題是二次函數(shù)的綜合題,考查了利用待定系數(shù)法求二次函數(shù)和一次函數(shù)的解析式,并能利用方程組求出兩圖象的交點(diǎn),把方程和函數(shù)有機(jī)地結(jié)合在一起,使函數(shù)問(wèn)題簡(jiǎn)單化;同時(shí)考查了分類(lèi)討論的思想,這一思想在二次函數(shù)中經(jīng)常運(yùn)用,要熟練掌握;本題還與相似結(jié)合,利用相似三角形對(duì)應(yīng)邊的比來(lái)表示線(xiàn)段的長(zhǎng).


 亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案
亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系中,一螞蟻從原點(diǎn)O出發(fā),按向上、向右、向下、向右的方向依次不斷移動(dòng),每次移動(dòng)1個(gè)單位.其行走路線(xiàn)如圖.

(1)填寫(xiě)下列各點(diǎn)的坐標(biāo):A4( , ),A8( , );
(2)點(diǎn)A4n﹣1的坐標(biāo)(n是正整數(shù))為
(3)指出螞蟻從點(diǎn)A2013到點(diǎn)A2014的移動(dòng)方向.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC內(nèi)部的一個(gè)動(dòng)點(diǎn),且滿(mǎn)足∠PAB=∠PBC,則線(xiàn)段CP長(zhǎng)的最小值為( )
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖:已知在△ABC中,AB=AC,D為BC邊的中點(diǎn),過(guò)點(diǎn)D作DE⊥AB,DF⊥AC,垂足分別為E,F(xiàn).

(1)求證:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知正方形ABCD的邊長(zhǎng)為1,點(diǎn)P為正方形內(nèi)一動(dòng)點(diǎn),若點(diǎn)M在AB上,且滿(mǎn)足△PBC∽△PAM,延長(zhǎng)BP交AD于點(diǎn)N,連結(jié)CM.
(1)如圖一,若點(diǎn)M在線(xiàn)段AB上,求證:AP⊥BN;AM=AN;
(2)①如圖二,在點(diǎn)P運(yùn)動(dòng)過(guò)程中,滿(mǎn)足△PBC∽△PAM的點(diǎn)M在AB的延長(zhǎng)線(xiàn)上時(shí),AP⊥BN和AM=AN是否成立?(不需說(shuō)明理由)
②是否存在滿(mǎn)足條件的點(diǎn)P,使得PC= ![]() ?請(qǐng)說(shuō)明理由.
?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC是一塊綠化帶,將陰影部分修建為花圃,已知AB=15,AC=9,BC=12,陰影部分是△ABC的內(nèi)切圓,一只自由飛翔的小鳥(niǎo)將隨機(jī)落在這塊綠化帶上,則小鳥(niǎo)落在花圃上的概率為( ) 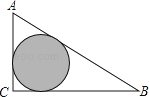
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩人進(jìn)行摸牌游戲.現(xiàn)有三張形狀大小完全相同的牌,正面分別標(biāo)有數(shù)字2,3,5.將三張牌背面朝上,洗勻后放在桌子上.
(1)甲從中隨機(jī)抽取一張牌,記錄數(shù)字后放回洗勻,乙再隨機(jī)抽取一張.請(qǐng)用列表法或畫(huà)樹(shù)狀圖的方法,求兩人抽取相同數(shù)字的概率;
(2)若兩人抽取的數(shù)字和為2的倍數(shù),則甲獲勝;若抽取的數(shù)字和為5的倍數(shù),則乙獲勝.這個(gè)游戲公平嗎?請(qǐng)用概率的知識(shí)加以解釋?zhuān)?/span>
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了落實(shí)省新課改精神,我是各校都開(kāi)設(shè)了“知識(shí)拓展類(lèi)”、“體藝特長(zhǎng)類(lèi)”、“實(shí)踐活動(dòng)類(lèi)”三類(lèi)拓展性課程,某校為了解在周二第六節(jié)開(kāi)設(shè)的“體藝特長(zhǎng)類(lèi)”中各門(mén)課程學(xué)生的參與情況,隨機(jī)調(diào)查了部分學(xué)生作為樣本進(jìn)行統(tǒng)計(jì),繪制了如圖所示的統(tǒng)計(jì)圖(部分信息未給出)
根據(jù)圖中信息,解答下列問(wèn)題:
(1)求被調(diào)查學(xué)生的總?cè)藬?shù);
(2)若該校有200名學(xué)生參加了“體藝特長(zhǎng)類(lèi)”中的各門(mén)課程,請(qǐng)估計(jì)參加棋類(lèi)的學(xué)生人數(shù);
(3)根據(jù)調(diào)查結(jié)果,請(qǐng)你給學(xué)校提一條合理化建議.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(探究)如圖①,在△ABC中,∠ABC的平分線(xiàn)與∠ACB的平分線(xiàn)相交于點(diǎn)P.
(1)若∠ABC=50°,∠ACB=80°,則∠A= 度,∠P= 度
(2)∠A與∠P的數(shù)量關(guān)系為 ,并說(shuō)明理由.
(應(yīng)用)如圖②,在△ABC中,∠ABC的平分線(xiàn)與∠ACB的平分線(xiàn)相交于點(diǎn)P.∠ABC的外角平分線(xiàn)與∠ACB的外角平分線(xiàn)相交于點(diǎn)Q.直接寫(xiě)出∠A與∠Q的數(shù)量關(guān)系為 .

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com