
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象相交于第一、三象限內的
的圖象相交于第一、三象限內的![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
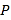
(1)求該反比例函數和一次函數的解析式;
(2)直接寫出當![]() 時,
時,![]() 的取值范圍;
的取值范圍;
(3)在![]() 軸上找一點
軸上找一點![]() 使
使![]() 最大,求
最大,求![]() 的最大值及點
的最大值及點![]() 的坐標.
的坐標.
【答案】(1)![]() ;
;![]() ;(2)當
;(2)當![]() 時,
時,![]() 或
或![]() ;(3)PBPC的最大值
;(3)PBPC的最大值![]() ,
,![]() .
.
【解析】
(1)將A點代入反比例函數表達式中即可求反比例函數得解析式,然后求出B的坐標,將A,B代入一次函數表達式中即可求一次函數的解析式;
(2)結合圖象和兩交點即可直接寫出當![]() 時,
時,![]() 的取值范圍;
的取值范圍;
(3)當P,B,C在一條直線上時,![]() 最大,此時P點為一次函數與y軸的交點,最大距離為BC的長度,再根據B,C兩點求BC的長度即可.
最大,此時P點為一次函數與y軸的交點,最大距離為BC的長度,再根據B,C兩點求BC的長度即可.
(1)把![]() 代入
代入![]() ,可得
,可得![]() ,
,
∴反比例函數的解析式為![]() ;
;
把點![]() 代入
代入![]() ,可得
,可得![]() ,
,
∴![]()
把![]() ,
,![]() 代入
代入![]() ,
,
可得![]() ,解得
,解得![]() ,
,
∴一次函數的解析式為![]() ;
;
(2)當![]() 時,
時,![]() 或
或![]() .
.
(3)一次函數的解析式為![]() ,令
,令![]() ,則
,則![]() ,
,
∴一次函數與![]() 軸的交點為
軸的交點為![]() ,
,
此時,![]() 最大,
最大,![]() 即為所求,
即為所求,
令![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑作⊙O,點D在⊙O上,BD=BC,DE⊥AC,垂足為點E,DE與⊙O和AB分別交于點M、F.連接BO、DO、AM.
(1)證明:BD是⊙O的切線;
(2)若tan∠AMD=![]() ,AD=2
,AD=2![]() ,求⊙O的半徑長;
,求⊙O的半徑長;
(3)在(2)的條件下,求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,∠B=60°,△ADE可以由△ABC繞點 A順時針旋轉90°得到,點D 與點B是對應點,點E與點C是對應點),連接CE,則∠CED的度數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
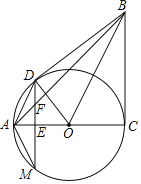
【題目】已知:四邊形 ABCD 內接于⊙O,連接 AC、BD,∠BAD+2∠ACB=180°.
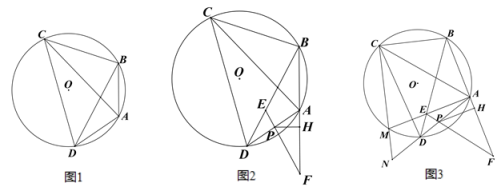
(1)如圖 1,求證:點 A 為弧 BD 的中點;
(2)如圖 2,點 E 為弦 BD 上一點,延長 BA 至點 F,使得 AF=AB,連接 FE 交 AD 于點 P,過點 P 作 PH⊥AF 于點 H,AF=2AH+AP,求證:AH:AB=PE:BE;
(3)在(2)的條件下,如圖 3,連接 AE,并延長 AE 交⊙O 于點 M,連接 CM,并延長 CM 交 AD 的延長線于點 N,連接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的長.
,求 AH 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 是關于
是關于![]() 的函數,若其函數圖象經過點
的函數,若其函數圖象經過點![]() ,則稱點
,則稱點![]() 為函數圖象上的“郡點”,例如:
為函數圖象上的“郡點”,例如:![]() 上存在“郡點”
上存在“郡點”![]() .
.
(1)直線___________(填寫直線解析式)上的每一個點都是“郡點”,雙曲線![]() 上的“郡點”是___________;
上的“郡點”是___________;
(2)若拋物線![]() 上有“郡點”,且“郡點”
上有“郡點”,且“郡點”![]() 、
、![]() (點
(點![]() 和點
和點![]() 可以重合)的坐標為
可以重合)的坐標為![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
(3)若函數![]() 的圖象上存在唯一的一個“郡點”,且當
的圖象上存在唯一的一個“郡點”,且當![]() ,
,![]() 的最小值
的最小值![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
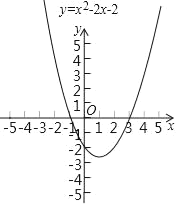
【題目】在實際問題中往往需要求得方程的近似解,這個時候,我們通常利用函數的圖象來完成.如,求方程x2﹣2x﹣2=0的實數根的近似解,觀察函數y=x2﹣2x﹣2的圖象,發現,當自變量為2時,函數值小于0(點(2,﹣2)在x軸下方),當自變量為3時,函數值大于0(點(3,1)在x軸上方).因為拋物線y=x2﹣2x﹣2是一條連續不斷的曲線,所以拋物線y=x2﹣2x﹣2在2<x<3這一段經過x軸,也就是說,當x取2、3之間的某個值時,函數值為0,即方程x2﹣2x﹣2=0在2、3之間有根.進一步,我們取2和3的平均數2.5,計算可知,對應的數值為﹣0.75,與自變量為3的函數值異號,所以這個根在2.5與3之間任意一個數作為近似解,該近似解與真實值的差都不會大于3﹣2.5=0.5.重復以上操作,隨著操作次數增加,根的近似值越來越接近真實值.用以上方法求得方程x2﹣2x﹣2=0的小于0的解,并且使得所求的近似解與真實值的差不超過0.3,該近似解為_____
查看答案和解析>>
科目:初中數學 來源: 題型:
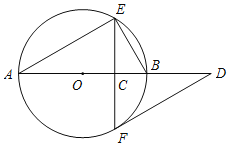
【題目】如圖,AB是⊙O的直徑,弦EF⊥AB于點C,過點F作⊙O的切線交AB的延長線于點D.
(1)已知∠A=α,求∠D的大小(用含α的式子表示);
(2)取BE的中點M,連接MF,請補全圖形;若∠A=30°,MF=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,網格中每個小正方形的邊長為1,點A,B均在格點上.則線段AB的長為 .請借助網格,僅用無刻度的直尺在AB上作出點P,使AP=![]() .
.
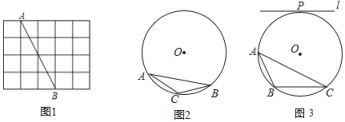
(2)⊙O為△ABC的外接圓,請僅用無刻度的直尺,依下列條件分別在圖2,圖3的圓中畫出一條弦,使這條弦將△ABC分成面積相等的兩部分(保留作圖痕跡,不寫作法,請下結論注明你所畫的弦).
①如圖2,AC=BC;
②如圖3,P為圓上一點,直線l⊥OP且l∥BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
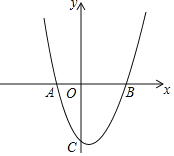
【題目】如圖,在平面直角坐標系中,已知拋物線y=![]() x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.
x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.
(1)求該拋物線的解析式及點C的坐標;
(2)直線y=﹣x﹣2與該拋物線在第四象限內交于點D,與x軸交于點F,連接AC,CD,線段AC與線段DF交于點G,求證:△AGF≌△CGD;
(3)直線y=m(m>0)與該拋物線的交點為M,N(點M在點N的左側),點M關于y軸的對稱點為點M′,點H的坐標為(1,0),若四邊形NHOM′的面積為![]() ,求點H到OM′的距離d.
,求點H到OM′的距離d.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com