
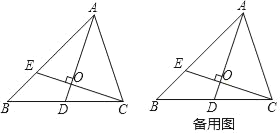
【題目】如圖,△ABC中,D是邊BC的中點(diǎn),E是AB邊上一點(diǎn),且AD⊥CE于O,AD=AC=CE.
(1)求證:∠B=45°;
(2)求![]() 的值;
的值;
(3)直接寫(xiě)出![]() 的值.
的值.
【答案】(1)見(jiàn)解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)作AF⊥BC于F,由等腰三角形的性質(zhì)得出DF=CF,∠ADC=∠ACD,∠CEA=∠EAC,證出∠1=∠2,∠B=∠EAF,即可得出結(jié)論;
(2)設(shè)DF=CF=m,則BC=4m,AF=BF=3m,由勾股定理得:CE=AD=![]() m,由三角形面積公式先得出AD×OC=CD×AF,求出OC=
m,由三角形面積公式先得出AD×OC=CD×AF,求出OC=![]() m,得出OE=CE﹣OC=
m,得出OE=CE﹣OC=![]() m,即可得出結(jié)果;
m,即可得出結(jié)果;
(3)作EG⊥BC于G,則△BEG是等腰直角三角形,得出EG=BG,設(shè)EG=BG=x,則CG=4m﹣x,在Rt△CEG中,由勾股定理得出方程,解方程得出EG=m,BE=![]() m,即可得出結(jié)果.
m,即可得出結(jié)果.
(1)證明:作AF⊥BC于F,如圖1所示:
∵AD=AC=CE,
∴DF=CF,∠ADC=∠ACD,∠CEA=∠EAC,
∵∠1+∠ADC=90°,∠ACD+∠2=90°,
∴∠1=∠2,
∵∠B+∠1=∠CEA=∠EAC=∠EAF+∠2,
∴∠B=∠EAF,
∵∠B+∠EAF=90°,
∴∠B=∠EAF=45°;
(2)解:設(shè)DF=CF=m,則BC=4m,AF=BF=3m,
由勾股定理得:CE=AD=![]() m,
m,
∵△ACD的面積=![]() AD×OC=
AD×OC=![]() CD×AF,
CD×AF,
∴AD×OC=CD×AF,
即OC×![]() m=2m×3m,
m=2m×3m,
∴OC=![]() m,
m,
∴OE=CE﹣OC=![]() m﹣
m﹣![]() m=
m=![]() m,
m,
∴![]() =
=![]() ;
;
(3)解:作EG⊥BC于G,如圖2所示:
則△BEG是等腰直角三角形,
∴EG=BG,
設(shè)EG=BG=x,則CG=4m﹣x,
在Rt△CEG中,由勾股定理得:x2+(4m﹣x)2=(![]() m)2,
m)2,
解得:x=m,或x=3m(舍去),
∴EG=m,
∴BE=![]() m,
m,
∴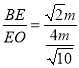 =
=![]() .
.



 數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案
數(shù)學(xué)奧賽暑假天天練南京大學(xué)出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】商場(chǎng)銷(xiāo)售一批襯衫,每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,為了擴(kuò)大 銷(xiāo)售,決定采取適當(dāng)?shù)慕祪r(jià)措施,經(jīng)調(diào)查發(fā)現(xiàn),如果一件襯衫每降價(jià)
元,為了擴(kuò)大 銷(xiāo)售,決定采取適當(dāng)?shù)慕祪r(jià)措施,經(jīng)調(diào)查發(fā)現(xiàn),如果一件襯衫每降價(jià)![]() 元,每天 可多售出
元,每天 可多售出![]() 件。設(shè)每件襯衫降價(jià)
件。設(shè)每件襯衫降價(jià)![]() 元,每天盈利
元,每天盈利![]() 元.
元.
![]() 求出
求出![]() 與
與![]() 之間的函數(shù)關(guān)系式;(不需寫(xiě)自變量的取值范圍).
之間的函數(shù)關(guān)系式;(不需寫(xiě)自變量的取值范圍).
![]() 出每件襯衫降價(jià)多少元時(shí),商場(chǎng)每天的盈利達(dá)到最大?盈利最大是多少元?
出每件襯衫降價(jià)多少元時(shí),商場(chǎng)每天的盈利達(dá)到最大?盈利最大是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1是一款優(yōu)雅且穩(wěn)定的拋物線型落地?zé)簦阑菽?/span>C為拋物線支架的最高點(diǎn),燈罩D距離地面1.86米,點(diǎn)最高點(diǎn)C距燈柱的水平距離為1.6米,燈柱AB及支架的相關(guān)數(shù)據(jù)如圖2所示.若茶幾擺放在燈罩的正下方,則茶幾到燈柱的距離AE為__米.
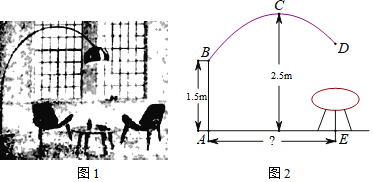
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】若關(guān)于x,y的二元一次方程組![]() 的解均為正整數(shù),m也是正整數(shù),則滿足條件的所有m值的和為____.
的解均為正整數(shù),m也是正整數(shù),則滿足條件的所有m值的和為____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
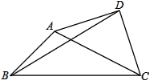
【題目】已知△ABC中,∠ABC=45°,AB=7![]() ,BC=17,以AC為斜邊在△ABC外作等腰Rt△ACD,連接BD,則BD的長(zhǎng)為___.
,BC=17,以AC為斜邊在△ABC外作等腰Rt△ACD,連接BD,則BD的長(zhǎng)為___.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某廠銷(xiāo)售一種茶壺和茶杯,茶壺每只定價(jià)40元,茶懷每只定價(jià)5元.廠方在開(kāi)展促銷(xiāo)活動(dòng)期間,向客戶提供兩種優(yōu)惠方案:①茶壺和茶杯都按定價(jià)的90%付款;②買(mǎi)一個(gè)茶壺送一個(gè)茶杯.現(xiàn)某客戶要到該廠購(gòu)買(mǎi)![]() 個(gè)茶壺(
個(gè)茶壺(![]() ),茶杯個(gè)數(shù)是茶壺?cái)?shù)的4倍少5.
),茶杯個(gè)數(shù)是茶壺?cái)?shù)的4倍少5.
(1)若該客戶按方案①購(gòu)買(mǎi),需付款______元(用含![]() 的代數(shù)式表示);若該客戶按方案②購(gòu)買(mǎi).需付款______元;(用含
的代數(shù)式表示);若該客戶按方案②購(gòu)買(mǎi).需付款______元;(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)若![]() ,通過(guò)計(jì)算說(shuō)明此時(shí)按哪種方案購(gòu)買(mǎi)較為合算?
,通過(guò)計(jì)算說(shuō)明此時(shí)按哪種方案購(gòu)買(mǎi)較為合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y=-x2+bx+c經(jīng)過(guò)點(diǎn)(0,6),其對(duì)稱(chēng)軸為直線x=![]() .在x軸上方作平行于x軸的直線l與拋物線交于A、B兩點(diǎn)(點(diǎn)A在對(duì)稱(chēng)軸的右側(cè)),過(guò)點(diǎn)A、B作x軸的垂線,垂足分別為D、C.設(shè)A點(diǎn)的橫坐標(biāo)為m.
.在x軸上方作平行于x軸的直線l與拋物線交于A、B兩點(diǎn)(點(diǎn)A在對(duì)稱(chēng)軸的右側(cè)),過(guò)點(diǎn)A、B作x軸的垂線,垂足分別為D、C.設(shè)A點(diǎn)的橫坐標(biāo)為m.

(1)求此拋物線所對(duì)應(yīng)的函數(shù)關(guān)系式.
(2)當(dāng)m為何值時(shí),矩形ABCD為正方形.
(3)當(dāng)m為何值時(shí),矩形ABCD的周長(zhǎng)最大,并求出這個(gè)最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() , 以
, 以![]() 為圓心,以
為圓心,以![]() 為半徑的圓與
為半徑的圓與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() ,與
,與![]() 軸正半軸相交于點(diǎn)
軸正半軸相交于點(diǎn)![]() 過(guò)
過(guò)![]() 作
作![]() ,點(diǎn)
,點(diǎn)![]() 為弦
為弦![]() 上一點(diǎn),連接
上一點(diǎn),連接![]() .
.
(1)求![]() 的長(zhǎng)度;
的長(zhǎng)度;
(2)求證;直線![]() 是⊙
是⊙![]() 的切線;
的切線;
(3)若點(diǎn)![]() 是弧
是弧![]() 上一動(dòng)點(diǎn)(
上一動(dòng)點(diǎn)(![]() 點(diǎn)與
點(diǎn)與![]() 點(diǎn)不重合),過(guò)點(diǎn)
點(diǎn)不重合),過(guò)點(diǎn)![]() 的
的![]() 的切線
的切線![]() 交
交![]() 軸于
軸于![]() ,若
,若![]() 為直角三角形,試求出所有符合條件的點(diǎn)
為直角三角形,試求出所有符合條件的點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
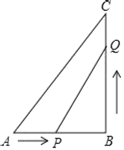
【題目】已知:如圖,在△ABC中,∠B=90°,AB=5cm,BC=7cm.點(diǎn)P從點(diǎn)A開(kāi)始沿AB邊向點(diǎn)B以1cm/s的速度移動(dòng),點(diǎn)Q從點(diǎn)B開(kāi)始沿BC邊向點(diǎn)C以2cm/s的速度移動(dòng).如果P,Q分別從A,B同時(shí)出發(fā).
(1)幾秒后,△PBQ的面積等于6cm2?
(2)幾秒后,四邊形APQC的面積最小?最小值是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com