【題目】下列運算，計算結果是錯誤的是（ ）
A.a4·a3=a7B.a6÷a3=a3C.(a3)2=a5D.a3·b3=(a·b)3
科目：初中數學 來源： 題型：
【題目】如圖，在等邊△
中， 
，當直角三角板
的
角的頂點
在
上移動時，斜邊
始終經過
邊的中點
，設直角三角板的另一直角邊
與
相交于點E.設
， 
，那么
與
之間的函數圖象大致是( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖點D、E分別在等邊ΔABC邊BC、CA上，且CD=AE,聯結AD、 BE.
(1)求證：BE=AD；
(2)延長DA交BE于F,求∠BFD的度數.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列各數都是由四舍五入法得到的近似數，它們分別精確到哪一位？各有幾個有效數字？
（1）小紅的體重為45.0千克；
（2）小明的媽媽的年薪約為5萬元；
（3）月球軌道呈橢圓形，遠地點平均距離為4.055×105千米．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題共10分）AB和AC 相交于點A， BD和CD相交于點D，探究∠BDC與∠B 、 ∠C、∠BAC的關系．
小明是這樣做的：
解：以點A為端點作射線AD．
∵∠1是△ABD的外角，∴∠1= ∠B+∠BAD．
同理∠2=∠C+∠CAD．
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD．即∠BDC=∠B+∠C+∠BAC．
小英的思路是：延長BD交AC于點E．
（1）按小英的思路完成∠BDC=∠B+∠C+∠BAC這一結論．
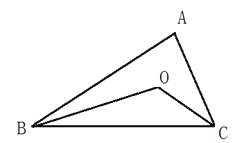
（2）按照上面的思路解決如下問題：如圖：在△ABC中，BE、CD分別是∠ABC∠ACB的角平分線，交AC于E，交AB于D．BE、CD相交于點O，∠A=60°．求∠BOC的度數．
（3）如圖：△ABC中，BO、CO分別是∠ABC與∠ACB的角平分線，且BO、CO相交于點O．猜想∠BOC與∠A有怎樣的關系，并加以證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若二次函數y=ax2+bx+c的x與y的部分對應值如下表：
| … | －4 | －3 | －2 | －1 | 0 | … |
| … | －5 | 0 | 3 | 4 | 3 | … |
（1）求此二次函數的表達式；
（2）畫出此函數圖象(不用列表).
（3）結合函數圖象，當－4＜x≤1時,寫出y的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的一元二次方程x2－(2k＋1)x＋k2＋k＝0.
(1)求證：方程有兩個不相等的實數根；
(2)若△ABC的兩邊AB，AC的長是這個方程的兩個實數根，第三邊BC的長為5，當△ABC是等腰三角形時，求k的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
