
【題目】如圖,在平面直角坐標系xOy中,點 ![]() 在直線
在直線 ![]() 上,過點
上,過點 ![]() 作
作 ![]() ∥y軸,交直線
∥y軸,交直線 ![]() 于點
于點 ![]() ,以
,以 ![]() 為直角頂點,
為直角頂點, ![]() 為直角邊,在
為直角邊,在 ![]() 的右側作等腰直角三角形
的右側作等腰直角三角形 ![]() ;再過點
;再過點 ![]() 作
作 ![]() ∥y軸,分別交直線
∥y軸,分別交直線 ![]() 和
和 ![]() 于
于 ![]() ,
, ![]() 兩點,以
兩點,以 ![]() 為直角頂點,
為直角頂點, ![]() 為直角邊,在
為直角邊,在 ![]() 的右側作等腰直角三角形
的右側作等腰直角三角形 ![]() ,…,按此規律進行下去,點
,…,按此規律進行下去,點 ![]() 的橫坐標為 , 點
的橫坐標為 , 點 ![]() 的橫坐標為 , 點
的橫坐標為 , 點 ![]() 的橫坐標為 . (用含n的式子表示,n為正整數)
的橫坐標為 . (用含n的式子表示,n為正整數)
【答案】3;![]() ;
;![]()
【解析】解:∵點 ![]() 在直線
在直線 ![]() 上,過點
上,過點 ![]() 作
作 ![]() ∥y軸,交直線
∥y軸,交直線 ![]() 于點
于點 ![]() ,
,
∴B1(2,1),
∴A1C1= A1B1=1,
∴C1(3,2).
∵A2B2∥y ,
∴A2(3,3), ![]() ,
,
∴A2C2= A2B2= ![]() ,
, ![]()
![]()
![]() ,即
,即 ![]() .
.
∵A3B3∥y , ![]() ,
, ![]() ,
,
∴A3C3= A3B3= ![]() ,
, ![]()
![]() ,即
,即 ![]() .
.
∴C1的橫坐標為![]() ;
;
C2的橫坐標為 ![]() ;
;
C3的橫坐標為 ![]() ;
;
……
∴Cn的橫坐標為 ![]() .
.
【考點精析】掌握數與式的規律和等腰直角三角形是解答本題的根本,需要知道先從圖形上尋找規律,然后驗證規律,應用規律,即數形結合尋找規律;等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°.


科目:初中數學 來源: 題型:
【題目】某種藥品原價為36元/盒,經過連續兩次降價后售價為25元/盒.設平均每次降價的百分率為x,根據題意所列方程正確的是( )
A.36(1﹣x)2=36﹣25
B.36(1﹣2x)=25
C.36(1﹣x)2=25
D.36(1﹣x2)=25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某城市按以下規定收取每月的水費:用水不超過10立方米,按每立方米2.1元收費;如果超過10立方米,超過部分按每立方米3元收費,已知某用戶l2月水費平均每立方米2.5元.
按要求回答下列問題:
(1)這個用戶12月用水量10立方米(填“超過”或“不超過”).
(2)在(1)的前提下,求12月這個用戶的用水量是多少立方米?
(3)該用戶12月份需交水費元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據招商引資網消息,為加快新區經濟發展,新區政府擬新區現代高效農業示范園區,共計劃投入資金3.75億元,精確到千萬位可表示為( )
A.3.7×108
B.3.8×108
C.0.38×1010
D.37×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線y=ax2﹣5ax+4a與x軸交于A、B(A點在B點的左側)與y軸交于點C.
(1)如圖1,連接AC、BC,若△ABC的面積為3時,求拋物線的解析式;
(2)如圖2,點P為第四象限拋物線上一點,連接PC,若∠BCP=2∠ABC時,求點P的橫坐標;
(3)如圖3,在(2)的條件下,點F在AP上,過點P作PH⊥x軸于H點,點K在PH的延長線上,AK=KF,∠KAH=∠FKH,PF=﹣4![]() a,連接KB并延長交拋物線于點Q,求PQ的長.
a,連接KB并延長交拋物線于點Q,求PQ的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖。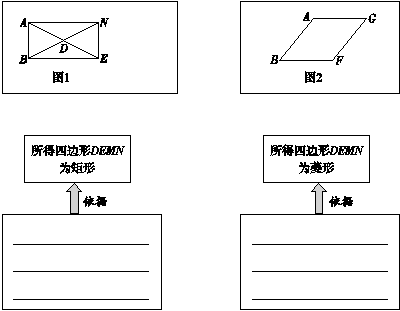
(1)畫圖-連線-寫依據:
先分別完成以下畫圖(不要求尺規作圖),再與判斷四邊形DEMN形狀的相應結論連線,并寫出判定依據(只將最后一步判定特殊平行四邊形的依據填在橫線上).
①如圖1,在矩形ABEN中,D為對角線的交點,過點N畫直線NP∥DE , 過點E畫直線EQ∥DN , NP與EQ的交點為點M , 得到四邊形DEMN;
②如圖2,在菱形ABFG中,順次連接四邊AB , BF , FG , GA的中點D , E , M , N , 得到四邊形DEMN.
(2)請從圖1、圖2的結論中選擇一個進行證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com