
【題目】安全使用電瓶車可以大幅度減少因交通事故引發的人身傷害,為此交警部門在全區范圍開展了安全使用電瓶車專項宣傳活動.在活動前和活動后分別隨機抽部分使用電瓶車的市民,就騎電瓶車戴安全帽情況(![]() :每次戴、
:每次戴、![]() :經常戴、
:經常戴、![]() :偶爾戴、
:偶爾戴、![]() :都不戴)進行問卷調查,將相關的數據制成如下統計圖表.
:都不戴)進行問卷調查,將相關的數據制成如下統計圖表.
活動前騎電瓶車戴安全帽情況統計表
類別 | 人數 |
| 68 |
| 245 |
| 510 |
| 177 |
合計 | 1000 |
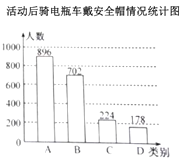
(1)宣傳活動前,在抽取的市民中哪一類別的人數最多?占抽取人數的百分之幾?
(2)該區約有37萬人使用電瓶車,請估計活動前全市騎電瓶車“都不戴”安全帽的總人數;
(3)小明認為,宣傳活動后騎電瓶車“都不戴”安全帽的人數為178,比活動前增加了1人,因此交警部門開展的宣傳活動沒有效果.小明分析數據的方法是否合理?請結合統計圖表,談談你對交警部門宣傳活動的效果的看法.
【答案】(1)C類偶爾戴的市民人數最多,占比為51%;(2)65490人;(3)小明分析數據的方法不合理,活動有效果.
【解析】
(1)根據圖表給出的數據得出“偶爾戴”(或C類)的人數最多,用“偶爾戴”的人數除以總人數即可得出答案;
(2)用該區的總人數乘以“都不戴”安全帽的人數所占的百分比即可;
(3)分別求出宣傳活動前后騎電瓶車“都不戴”安全帽所占的百分比,再進行比較,即可得出小明的分析不合理.
解:(1)C類偶爾戴的區民人數最多,占比為:![]() ×100%=51%;
×100%=51%;
(2)![]() ×370000=65490人,
×370000=65490人,
答:活動前全區騎電瓶車“都不戴”安全帽的總人數約有65490人;
(3)不合理.
活動開展前,“都不戴”占比為:![]() ×100%=17.7%,
×100%=17.7%,
“每次戴”占比為:![]() ×100%=6.8%,
×100%=6.8%,
活動開展后,“都不戴”占比為:![]() ×100%=8.9%,
×100%=8.9%,
“每次戴”占比為:![]() ×100%=44.8%,
×100%=44.8%,
∵“都不戴”的人數所占的百分比明顯下降,而“每次戴”百分比明顯上升,
∴說明活動有效果.


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的頂點A,B分別在y軸、x軸上,OA=2,OB=1,斜邊AC∥x軸.若反比例函數y![]() (k>0,x>0)的圖象經過AC的中點D,則k的值為( )
(k>0,x>0)的圖象經過AC的中點D,則k的值為( )

A.4B.5C.6D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知函數![]() 與函數
與函數![]() 定義新函數
定義新函數![]()
(1)若![]() 則新函數
則新函數![]() ;
;
(2)若新函數![]() 的解析式為
的解析式為![]() 則
則![]() ,
,![]() ;
;
(3)設新函數![]() 頂點為
頂點為![]() .
.
①當![]() 為何值時,
為何值時,![]() 有最大值,并求出最大值;
有最大值,并求出最大值;
②求![]() 與
與![]() 的函數解析式;
的函數解析式;
(4)請你探究:函數![]() 與新函數
與新函數![]() 分別經過定點
分別經過定點![]() ,函數
,函數![]() 的頂點為
的頂點為![]() ,新函數
,新函數![]() 上存在一點
上存在一點![]() ,使得以點
,使得以點![]() 為頂點的四邊形為平行四邊形時,直接寫出
為頂點的四邊形為平行四邊形時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
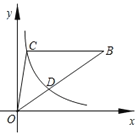
【題目】如圖,△OBC的邊BC∥x軸,過點C的雙曲線y=![]() (k≠0)與△OBC的邊OB交于點D,且OD:DB=1:2,若△OBC的面積等于8,則k的值為__.
(k≠0)與△OBC的邊OB交于點D,且OD:DB=1:2,若△OBC的面積等于8,則k的值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
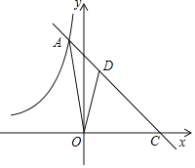
【題目】如圖,在平面直角坐標系xOy中,函數y=﹣x+5的圖象與函數y=![]() (k<0)的圖象相交于點A,并與x軸交于點C,S△AOC=15.點D是線段AC上一點,CD:AC=2:3.
(k<0)的圖象相交于點A,并與x軸交于點C,S△AOC=15.點D是線段AC上一點,CD:AC=2:3.
(1)求k的值;
(2)根據圖象,直接寫出當x<0時不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)求△AOD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
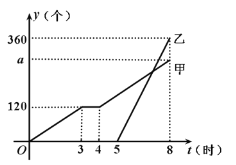
【題目】某天,甲車間工人加工零件,工作中有一次停產檢修機器,然后以原來的工作效率繼續加工,由于任務緊急,乙車間加入與甲車間一起生產零件,兩車間各自加工零件的數量y(個)與甲車間加工時間t(時)之間的函數圖象如圖所示.
(1)求乙車間加工零件的數量y與甲車間加工時間t之間的函數關系式,并寫出t的取值范圍.
(2)求甲車間加工零件總量a.
(3)當甲、乙兩車間加工零件總數量為320個時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每到春夏交替時節,楊樹的楊絮漫天飛舞,易引發皮膚病、呼吸道疾病等,給人們生活造成困擾,為了解市民對治理楊絮方法的贊同情況,某課題小組隨機調查了部分市民(調查問卷如下),并根據調查結果繪制了如下尚不完整的統計圖:
調查問卷
治理楊絮:您選哪一項? (每人只選一項)
A.減少楊樹新增面積,控制楊樹每年的栽種量;
B.調整樹種結構,逐漸更換現有楊樹;
C.選育無絮楊品種,并推廣種植;
D.對楊樹注射生物干擾素,避免產生飛絮;
E.其他.
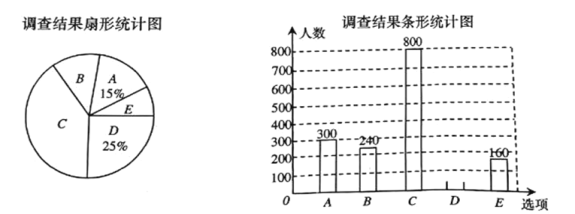
根據以上信息,解答下列問題:
(1)在扇形統計圖中,求扇形![]() 的圓心角度數;
的圓心角度數;
(2)補全條形統計圖;
(3)若該市約有![]() 萬人,請估計贊同“選育無絮楊品種,并推廣種植”的人數.
萬人,請估計贊同“選育無絮楊品種,并推廣種植”的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在菱形ABCD中,AB=4,∠BAD=120°,點P是直線AB上任意一點,聯結PC,在∠PCD內部作射線CQ與對角線BD交于點Q(與B、D不重合),且∠PCQ=30°.
(1)如圖,當點P在邊AB上時,如果BP=3,求線段PC的長;
(2)當點P在射線BA上時,設![]() ,求y關于
,求y關于![]() 的函數解析式及定義域;
的函數解析式及定義域;
(3)聯結PQ,直線PQ與直線BC交于點E,如果![]() 與
與![]() 相似,求線段BP的長.
相似,求線段BP的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com