
【題目】如圖1,經過原點O的拋物線![]() (a≠0)與x軸交于另一點A(
(a≠0)與x軸交于另一點A(![]() ,0),在第一象限內與直線y=x交于點B(2,t).
,0),在第一象限內與直線y=x交于點B(2,t).
(1)求這條拋物線的表達式;
(2)在第四象限內的拋物線上有一點C,滿足以B,O,C為頂點的三角形的面積為2,求點C的坐標;
(3)如圖2,若點M在這條拋物線上,且∠MBO=∠ABO,在(2)的條件下,是否存在點P,使得△POC∽△MOB?若存在,求出點P的坐標;若不存在,請說明理由.

【答案】(1)![]() ;(2)C(1,﹣1);(3)存在,P的坐標為(
;(2)C(1,﹣1);(3)存在,P的坐標為(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).
【解析】
試題分析:(1)由直線解析式可求得B點坐標,由A、B坐標,利用待定系數法可求得拋物線的表達式;
(2)過C作CD∥y軸,交x軸于點E,交OB于點D,過B作BF⊥CD于點F,可設出C點坐標,利用C點坐標可表示出CD的長,從而可表示出△BOC的面積,由條件可得到關于C點坐標的方程,可求得C點坐標;
(3)設MB交y軸于點N,則可證得△ABO≌△NBO,可求得N點坐標,可求得直線BN的解析式,聯立直線BM與拋物線解析式可求得M點坐標,過M作MG⊥y軸于點G,由B、C的坐標可求得OB和OC的長,由相似三角形的性質可求得![]() 的值,當點P在第一象限內時,過P作PH⊥x軸于點H,由條件可證得△MOG∽△POH,由
的值,當點P在第一象限內時,過P作PH⊥x軸于點H,由條件可證得△MOG∽△POH,由![]() =
=![]() =
=![]() 的值,可求得PH和OH,可求得P點坐標;當P點在第三象限時,同理可求得P點坐標.
的值,可求得PH和OH,可求得P點坐標;當P點在第三象限時,同理可求得P點坐標.
試題解析:
(1)∵B(2,t)在直線y=x上,∴t=2,∴B(2,2),把A、B兩點坐標代入拋物線解析式可得: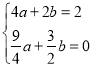 ,解得:
,解得:![]() ,∴拋物線解析式為
,∴拋物線解析式為![]() ;
;
(2)如圖1,過C作CD∥y軸,交x軸于點E,交OB于點D,過B作BF⊥CD于點F,∵點C是拋物線上第四象限的點,∴可設C(t,2t2﹣3t),則E(t,0),D(t,t),∴OE=t,BF=2﹣t,CD=t﹣(2t2﹣3t)=﹣2t2+4t,∴S△OBC=S△CDO+S△CDB=![]() CDOE+
CDOE+![]() CDBF=
CDBF=![]() (﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∵△OBC的面積為2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);
(﹣2t2+4t)(t+2﹣t)=﹣2t2+4t,∵△OBC的面積為2,∴﹣2t2+4t=2,解得t1=t2=1,∴C(1,﹣1);

(3)存在.設MB交y軸于點N,如圖2,∵B(2,2),∴∠AOB=∠NOB=45°,在△AOB和△NOB中,∵∠AOB=∠NOB,OB=OB,∠ABO=∠NBO,∴△AOB≌△NOB(ASA),∴ON=OA=![]() ,∴N(0,
,∴N(0,![]() ),∴可設直線BN解析式為y=kx+
),∴可設直線BN解析式為y=kx+![]() ,把B點坐標代入可得2=2k+
,把B點坐標代入可得2=2k+![]() ,解得k=
,解得k=![]() ,∴直線BN的解析式為
,∴直線BN的解析式為![]() ,聯立直線BN和拋物線解析式可得:
,聯立直線BN和拋物線解析式可得: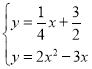 ,解得:
,解得:![]() 或
或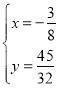 ,∴M(
,∴M(![]() ,
,![]() ),∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=
),∵C(1,﹣1),∴∠COA=∠AOB=45°,且B(2,2),∴OB=![]() ,OC=
,OC=![]() ,∵△POC∽△MOB,∴
,∵△POC∽△MOB,∴![]() =
=![]() =2,∠POC=∠BOM,當點P在第一象限時,如圖3,過M作MG⊥y軸于點G,過P作PH⊥x軸于點H,如圖3
=2,∠POC=∠BOM,當點P在第一象限時,如圖3,過M作MG⊥y軸于點G,過P作PH⊥x軸于點H,如圖3
∵∠COA=∠BOG=45°,∴∠MOG=∠POH,且∠PHO=∠MGO,∴△MOG∽△POH,∴![]() =
=![]() =
=![]() =2,∵M(
=2,∵M(![]() ,
,![]() ),∴MG=
),∴MG=![]() ,OG=
,OG=![]() ,∴PH=
,∴PH=![]() MG=
MG=![]() ,OH=
,OH=![]() OG=
OG=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
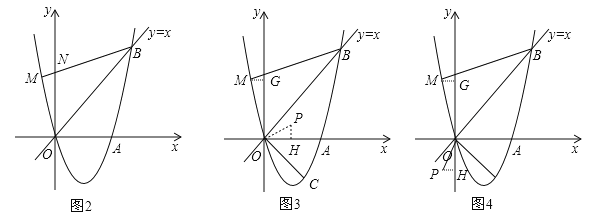
當點P在第三象限時,如圖4,過M作MG⊥y軸于點G,過P作PH⊥y軸于點H,同理可求得PH=![]() MG=
MG=![]() ,OH=
,OH=![]() OG=
OG=![]() ,∴P(﹣
,∴P(﹣![]() ,
,![]() );
);
綜上可知:存在滿足條件的點P,其坐標為(![]() ,
,![]() )或(﹣
)或(﹣![]() ,
,![]() ).
).


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,動點P從點B出發沿射線BC以1cm/s的速度移動,設運動的時間為t秒.

(1)求BC邊的長;
(2)當△ABP為直角三角形時,求t的值;
(3)當△ABP為等腰三角形時,求t的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校課程安排中,各班每天下午只安排三節課.
(1)初一(1)班星期二下午安排了數學、英語、生物課各一節,通過畫樹狀圖求出把數學課安排在最后一節的概率;
(2)星期三下午,初二(1)班安排了數學、物理、政治課各一節,初二(2)班安排了數學、語文、地理課各一節,此時兩班這六節課的每一種課表排法出現的概率是![]() .已知這兩個班的數學課都由同一個老師擔任,其他課由另外四位老師擔任.求這兩個班數學課不相沖突的概率.
.已知這兩個班的數學課都由同一個老師擔任,其他課由另外四位老師擔任.求這兩個班數學課不相沖突的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,![]()
(1) 如圖1,若BD=DC,點C在AE的垂直平分線上。AB+BD與DE有什么關系?請給出證明。
(2) 如圖2,若![]() , AB+BD與DE是否還存在(1)中的關系?若存在,請給出證明,若不存在,請說明理由。
, AB+BD與DE是否還存在(1)中的關系?若存在,請給出證明,若不存在,請說明理由。
(3) 若![]() ,則AB+AE與AD+BE有怎樣的關系?答:AB+AE AD+BE (填“>”,“<”或“=”)
,則AB+AE與AD+BE有怎樣的關系?答:AB+AE AD+BE (填“>”,“<”或“=”)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABDC是⊙O的內接四邊形,AB是⊙O的直徑,OD⊥BC于E.
(1)請你寫出四個不同類型的正確結論;
(2)若BE=4,AC=6,求DE的長.
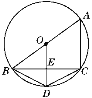
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A、C分別在x、y軸的正半軸上,點D為對角線OB的中點,點E(4,n)在邊AB上,反比例函數![]() (k≠0)在第一象限內的圖象經過點D、E,且tan∠BOA=
(k≠0)在第一象限內的圖象經過點D、E,且tan∠BOA=![]() .
.
(1)求邊AB的長;
(2)求反比例函數的解析式和n的值;
(3)若反比例函數的圖象與矩形的邊BC交于點F,將矩形折疊,使點O與點F重合,折痕分別與x、y軸正半軸交于點H、G,求線段OG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC在正方形網格中,若B(﹣3,﹣1),按要求回答下列問題:

(1)在圖中建立正確的平面直角坐標系;
(2)根據所建立的坐標系,寫出A和C的坐標;
(3)求△ABC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD與角平分線AE相交點F,過點C作CH⊥AE于G,交AB于H.
(1)求∠BCH的度數;
(2)求證:CE=BH.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】細心觀察圖形,認真分析各式,然后解答問題:
OA1=1;
OA2=![]() ; S1=
; S1=![]() ×1×1=
×1×1=![]() ;
;
OA3=![]() ; S2=
; S2=![]() ×
×![]() ×1=
×1=![]() ;
;
OA4=![]() ; S3=
; S3=![]() ×
×![]() ×1=
×1=![]() ;
;
(1)推算出OA10= .
(2)若一個三角形的面積是![]() .則它是第 個三角形.
.則它是第 個三角形.
(3)用含n(n是正整數)的等式表示上述面積變化規律;
(4)求出S12+S22+S23+…+S2100的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com