
【題目】今年植樹(shù)節(jié)期間,某景觀園林公司購(gòu)進(jìn)一批成捆的![]() ,
,![]() 兩種樹(shù)苗,每捆
兩種樹(shù)苗,每捆![]() 種樹(shù)苗比每捆
種樹(shù)苗比每捆![]() 種樹(shù)苗多10棵,每捆
種樹(shù)苗多10棵,每捆![]() 種樹(shù)苗和每捆
種樹(shù)苗和每捆![]() 種樹(shù)苗的價(jià)格分別是630元和600元,而每棵
種樹(shù)苗的價(jià)格分別是630元和600元,而每棵![]() 種樹(shù)苗和每棵
種樹(shù)苗和每棵![]() 種樹(shù)苗的價(jià)格分別是這一批樹(shù)苗平均每棵價(jià)格的0.9倍和1.2倍.
種樹(shù)苗的價(jià)格分別是這一批樹(shù)苗平均每棵價(jià)格的0.9倍和1.2倍.
(1)求這一批樹(shù)苗平均每棵的價(jià)格是多少元?
(2)如果購(gòu)進(jìn)的這批樹(shù)苗共5500棵,![]() 種樹(shù)苗至多購(gòu)進(jìn)3500棵,為了使購(gòu)進(jìn)的這批樹(shù)苗的費(fèi)用最低,應(yīng)購(gòu)進(jìn)
種樹(shù)苗至多購(gòu)進(jìn)3500棵,為了使購(gòu)進(jìn)的這批樹(shù)苗的費(fèi)用最低,應(yīng)購(gòu)進(jìn)![]() 種樹(shù)苗和
種樹(shù)苗和![]() 種樹(shù)苗各多少棵?并求出最低費(fèi)用.
種樹(shù)苗各多少棵?并求出最低費(fèi)用.
【答案】(1)這一批樹(shù)苗平均每棵的價(jià)格是20元;(2)購(gòu)進(jìn)![]() 種樹(shù)苗3500棵,
種樹(shù)苗3500棵,![]() 種樹(shù)苗2000棵,能使得購(gòu)進(jìn)這批樹(shù)苗的費(fèi)用最低為111000元.
種樹(shù)苗2000棵,能使得購(gòu)進(jìn)這批樹(shù)苗的費(fèi)用最低為111000元.
【解析】
(1)設(shè)這一批樹(shù)苗平均每棵的價(jià)格是![]() 元,分別表示出兩種樹(shù)苗的數(shù)量,根據(jù)“每捆
元,分別表示出兩種樹(shù)苗的數(shù)量,根據(jù)“每捆![]() 種樹(shù)苗比每捆
種樹(shù)苗比每捆![]() 種樹(shù)苗多10棵”列方程即可求解;
種樹(shù)苗多10棵”列方程即可求解;
(2)設(shè)購(gòu)進(jìn)![]() 種樹(shù)苗
種樹(shù)苗![]() 棵,這批樹(shù)苗的費(fèi)用為
棵,這批樹(shù)苗的費(fèi)用為![]() ,得到w與t的關(guān)系式,根據(jù)題意得到t的取值范圍,根據(jù)函數(shù)增減性即可求解.
,得到w與t的關(guān)系式,根據(jù)題意得到t的取值范圍,根據(jù)函數(shù)增減性即可求解.
解:(1)設(shè)這一批樹(shù)苗平均每棵的價(jià)格是![]() 元,
元,
根據(jù)題意,得![]() ,
,
解之,得![]() .
.
經(jīng)檢驗(yàn)知,![]() 是原分式方程的根,并符合題意.
是原分式方程的根,并符合題意.
答:這一批樹(shù)苗平均每棵的價(jià)格是20元.
(2)由(1)可知![]() 種樹(shù)苗每棵價(jià)格為
種樹(shù)苗每棵價(jià)格為![]() 元,種樹(shù)苗每棵價(jià)格為
元,種樹(shù)苗每棵價(jià)格為![]() 元,
元,
設(shè)購(gòu)進(jìn)![]() 種樹(shù)苗
種樹(shù)苗![]() 棵,這批樹(shù)苗的費(fèi)用為
棵,這批樹(shù)苗的費(fèi)用為![]() ,則
,則
![]() .
.
∵![]() 是
是![]() 的一次函數(shù),
的一次函數(shù),![]() ,
,![]() 隨著
隨著![]() 的增大而減小,
的增大而減小,![]() ,
,
∴當(dāng)![]() 棵時(shí),
棵時(shí),![]() 最小.此時(shí),
最小.此時(shí),![]() 種樹(shù)苗有
種樹(shù)苗有![]() 棵,
棵,![]() .
.
答:購(gòu)進(jìn)![]() 種樹(shù)苗3500棵,
種樹(shù)苗3500棵,![]() 種樹(shù)苗2000棵,能使得購(gòu)進(jìn)這批樹(shù)苗的費(fèi)用最低為111000元.
種樹(shù)苗2000棵,能使得購(gòu)進(jìn)這批樹(shù)苗的費(fèi)用最低為111000元.


 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案 陽(yáng)光考場(chǎng)單元測(cè)試卷系列答案
陽(yáng)光考場(chǎng)單元測(cè)試卷系列答案 名校聯(lián)盟沖刺卷系列答案
名校聯(lián)盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
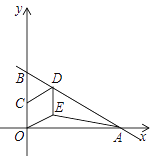
【題目】如圖,直線![]() 與x軸、y軸分別交于A,B兩點(diǎn),C是OB的中點(diǎn),D是AB上一點(diǎn),四邊形OEDC是菱形,則△OAE的面積為________.
與x軸、y軸分別交于A,B兩點(diǎn),C是OB的中點(diǎn),D是AB上一點(diǎn),四邊形OEDC是菱形,則△OAE的面積為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線![]() ,
,![]() ,
,![]() ,…,
,…,![]() (n為正整數(shù)),點(diǎn)A(0,1).
(n為正整數(shù)),點(diǎn)A(0,1).
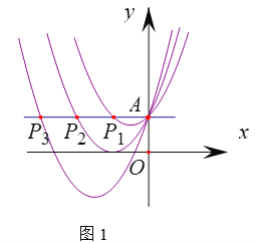
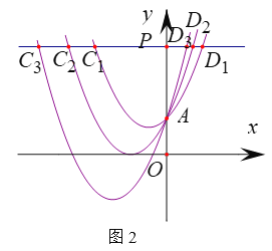
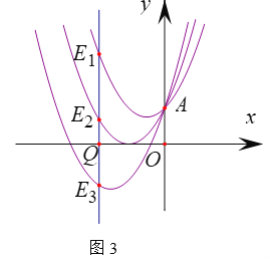
(1)如圖1,過(guò)點(diǎn)A作y軸垂線,分別交拋物線![]() ,
,![]() ,
,![]() ,…,
,…,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,
,![]() ,…,
,…,![]() (
(![]() 和點(diǎn)A不重合).
和點(diǎn)A不重合).
①求![]() 的長(zhǎng).
的長(zhǎng).
②求![]() 的長(zhǎng).
的長(zhǎng).
(2)如圖2,點(diǎn)P從點(diǎn)A出發(fā),沿y軸向上運(yùn)動(dòng),過(guò)點(diǎn)P作y軸的垂線,交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,交拋物線
,交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,交拋物線
,交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,……,交拋物線
,……,交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() (
(![]() 在第二象限).
在第二象限).
①求![]() 的值.
的值.
②求![]() 的值.
的值.
(3)過(guò)x軸上的點(diǎn)Q(原點(diǎn)除外),作x軸的垂線分別交拋物線![]() ,
,![]() ,
,![]() ,…,
,…,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,是否存在線段
,是否存在線段![]() (i,j為正整數(shù)),使
(i,j為正整數(shù)),使![]() ,若存在,求出i+j的最小值;若不存在,說(shuō)明理由.
,若存在,求出i+j的最小值;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線![]() 交x軸于
交x軸于![]() ,
,![]() 兩點(diǎn),與y軸交于點(diǎn)C,AC,BC.M為線段OB上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)M作
兩點(diǎn),與y軸交于點(diǎn)C,AC,BC.M為線段OB上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)M作![]() 軸,交拋物線于點(diǎn)P,交BC于點(diǎn)Q.
軸,交拋物線于點(diǎn)P,交BC于點(diǎn)Q.
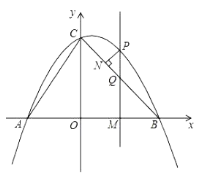
(1)求拋物線的表達(dá)式;
(2)過(guò)點(diǎn)P作![]() ,垂足為點(diǎn)N.設(shè)M點(diǎn)的坐標(biāo)為
,垂足為點(diǎn)N.設(shè)M點(diǎn)的坐標(biāo)為![]() ,請(qǐng)用含m的代數(shù)式表示線段PN的長(zhǎng),并求出當(dāng)m為何值時(shí)PN有最大值,最大值是多少?
,請(qǐng)用含m的代數(shù)式表示線段PN的長(zhǎng),并求出當(dāng)m為何值時(shí)PN有最大值,最大值是多少?
(3)試探究點(diǎn)M在運(yùn)動(dòng)過(guò)程中,是否存在這樣的點(diǎn)Q,使得以A,C,Q為頂點(diǎn)的三角形是等腰三角形.若存在,請(qǐng)求出此時(shí)點(diǎn)Q的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知拋物線經(jīng)過(guò)點(diǎn)A(﹣1,0)、B(3,0)、C(0,3)三點(diǎn).
(1)求拋物線的解析式.
(2)點(diǎn)M是線段BC上的點(diǎn)(不與B,C重合),過(guò)M作MN∥y軸交拋物線于N,若點(diǎn)M的橫坐標(biāo)為m,請(qǐng)用m的代數(shù)式表示MN的長(zhǎng).
(3)在(2)的條件下,連接NB、NC,是否存在m,使△BNC的面積最大?若存在,求m的值;若不存在,說(shuō)明理由.
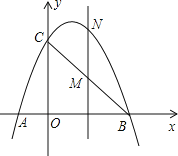
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC為正三角形,BD是角平分線,點(diǎn)F在線段BD上移動(dòng),直線CF與AB交于點(diǎn)E,連結(jié)AF,當(dāng)AE=AF時(shí),∠BCE=_____度.
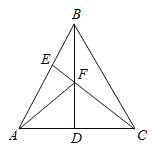
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:如果將△ABC與△DEF各分割成兩個(gè)三角形,且△ABC所分的兩個(gè)三角形與△DEF所分的兩個(gè)三角形分別對(duì)應(yīng)相似,那么稱(chēng)△ABC與△DEF互為“近似三角形”,將每條分割線稱(chēng)為“近似分割線”.
(1)如圖1,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,∠A=30°,∠D=40°,請(qǐng)判斷這兩個(gè)三角形是否互為“近似三角形”?如果是,請(qǐng)直接在圖1中畫(huà)出一組分割線,并注明分割后所得兩個(gè)小三角形銳角的度數(shù);若不是,請(qǐng)說(shuō)明理由.
(2)判斷下列命題是真命題還是假命題,若是真命題,請(qǐng)?jiān)诶ㄌ?hào)內(nèi)打“√”;若是假命題,請(qǐng)?jiān)诶ㄌ?hào)內(nèi)打“×”.
①任意兩個(gè)直角三角形都是互為“近似三角形” ;
②兩個(gè)“近似三角形”只有唯一的“近似分割線” ;
③如果兩個(gè)三角形中有一個(gè)角相等,那么這兩個(gè)三角形一定是互為“近似三角形” .
(3)如圖2,已知△ABC與△DEF中,∠A=∠D=15°,∠B=45°,∠E=60°,且BC=EF=![]()
![]() ,判斷這兩個(gè)三角形是否互為“近似三角形”?如果是,請(qǐng)?jiān)趫D2中畫(huà)出不同位置的“近似分割線”,并直接分別寫(xiě)出“近似分割線”的和;如果不是,請(qǐng)說(shuō)明理由.
,判斷這兩個(gè)三角形是否互為“近似三角形”?如果是,請(qǐng)?jiān)趫D2中畫(huà)出不同位置的“近似分割線”,并直接分別寫(xiě)出“近似分割線”的和;如果不是,請(qǐng)說(shuō)明理由.
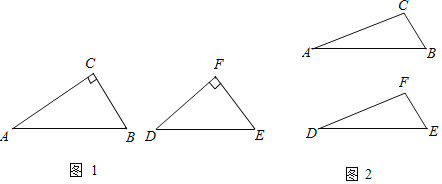
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
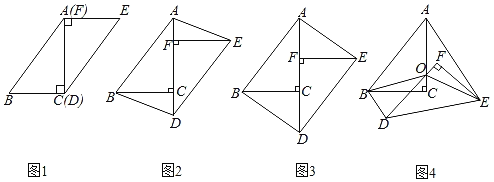
【題目】在一次數(shù)學(xué)研究性學(xué)習(xí)中,小兵將兩個(gè)全等的直角三角形紙片ABC和DEF拼在一起,使點(diǎn)A與點(diǎn)F重合,點(diǎn)C與點(diǎn)D重合(如圖1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并進(jìn)行如下研究活動(dòng).
活動(dòng)一:將圖1中的紙片DEF沿AC方向平移,連結(jié)AE,BD(如圖2),當(dāng)點(diǎn)F與點(diǎn)C重合時(shí)停止平移.
(思考)圖2中的四邊形ABDE是平行四邊形嗎?請(qǐng)說(shuō)明理由.
(發(fā)現(xiàn))當(dāng)紙片DEF平移到某一位置時(shí),小兵發(fā)現(xiàn)四邊形ABDE為矩形(如圖3).求AF的長(zhǎng).
活動(dòng)二:在圖3中,取AD的中點(diǎn)O,再將紙片DEF繞點(diǎn)O順時(shí)針?lè)较蛐D(zhuǎn)α度(0≤α≤90),連結(jié)OB,OE(如圖4).
(探究)當(dāng)EF平分∠AEO時(shí),探究OF與BD的數(shù)量關(guān)系,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】珠海市有A,B,C,D,E五個(gè)景區(qū)很受游客喜愛(ài).對(duì)某小區(qū)居民在暑假期間去以上五個(gè)景區(qū)旅游(只選一個(gè)景區(qū))的意向做了一次隨機(jī)調(diào)查統(tǒng)計(jì),并根據(jù)這個(gè)統(tǒng)計(jì)結(jié)果制作了如下兩幅不完整的統(tǒng)計(jì)圖.
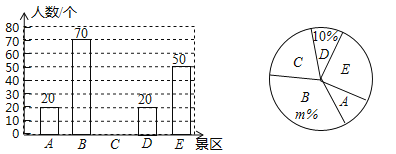
(1)該小區(qū)居民在這次隨機(jī)調(diào)查中被調(diào)查到的人數(shù)是 人,m= ;
(2)若該小區(qū)有居民1500人,試估計(jì)去C景區(qū)旅游的居民約有多少人?
(3)甲、乙兩人暑假打算游玩,甲從B、C兩個(gè)景點(diǎn)中任意選擇一個(gè)游玩,乙從B、C 、E三個(gè)景點(diǎn)中任意選擇一個(gè)游玩.求甲、乙恰好游玩同一景點(diǎn)的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com