
【題目】已知關于x的方程x2﹣2(m+1)x+m2﹣3=0.
(1)當m取何值時,方程有兩個不相等的實數根?
(2)設x1、x2是方程的兩根,且x12+x22=22+x1x2,求實數m的值.
【答案】(1)m>﹣2;(2)實數m的值為1.
【解析】分析:
(1)根據“一元二次方程![]() 中,當根的判別式△=
中,當根的判別式△=![]() 時,方程有兩個不相等的實數根”列出不等式進行解答即可;
時,方程有兩個不相等的實數根”列出不等式進行解答即可;
(2)根據“一元二次方程根與系數的關系”可得![]() ,將所得等式代入x12+x22=22+x1x2中得到關于m的方程,并結合(1)中所得m的取值范圍即可求得m的值.
,將所得等式代入x12+x22=22+x1x2中得到關于m的方程,并結合(1)中所得m的取值范圍即可求得m的值.
詳解:
(1)由題意可得:在關于x的方程x2﹣2(m+1)x+m2﹣3=0中,
△=[﹣2(m+1)]2﹣4(m2﹣3)=8m+16,
∵關于x的方程x2﹣2(m+1)x+m2﹣3=0有兩個不相等的實數根時,
∴△>0,即8m+16>0,解得m>﹣2;
(2)根據一元二次方程根與系數之間的關系,
得x1+x2=2(m+1),x1x2=m2﹣3,
∵x12+x22=22+x1x2=(x1+x2)2﹣2x1x2,
∴[2(m+1)]﹣2(m2﹣3)=6+(m2﹣3),
化簡,得m2+8m﹣9=0,解得m=1或m=﹣9(不合題意,舍去),
∴實數m的值為1.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀材料:
小明在學習二次根式后,發現一些含根號的式子可以寫成另一個式子的平方,如![]() .善于思考的小明進行了以下探索:
.善于思考的小明進行了以下探索:
設![]() (其中
(其中![]() 、
、![]() 、
、![]() 、
、![]() 均為整數),則有
均為整數),則有![]() .
.
![]() ,
,![]() .這樣小明就找到了一種把類似
.這樣小明就找到了一種把類似![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
(1)當![]() 、
、![]() 、
、![]() 、
、![]() 均為正整數時,若
均為正整數時,若![]() ,用含
,用含![]() 、
、![]() 的式子分別表示
的式子分別表示![]() 、
、![]() ,得:
,得:![]() ,
,![]() ;
;
(2)利用所探索的結論,找一組正整數![]() 、
、![]() 、
、![]() 、
、![]() 填空:
填空: ![]()
![]()
![]()
![]()
![]() ;
;
(3)若![]() ,且
,且![]() 、
、![]() 、
、![]() 均為正整數,求
均為正整數,求![]() 的值?
的值?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電信公司有A、B兩種計費方案:月通話費用y(元)與通話時間x(分鐘)的關系,如圖所示,下列說法中正確的是( )
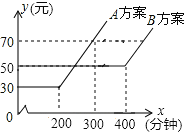
A.月通話時間低于200分鐘選B方案劃算
B.月通話時間超過300分鐘且少于400分鐘選A方案劃算
C.月通話費用為70元時,A方案比B方案的通話時間長
D.月通話時間在400分鐘內,B方案通話費用始終是50元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,
,![]() 是多項式
是多項式![]() 的一次項系數,
的一次項系數,![]() 是絕對值最小的整數,單項式
是絕對值最小的整數,單項式![]() 的次數為
的次數為![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若將數軸在點![]() 處折疊,則點
處折疊,則點![]() 與點
與點![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)點![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒1個單位長度的速度向右運動,同時,點
以每秒1個單位長度的速度向右運動,同時,點![]() 和點
和點![]() 分別以每秒3個單位長度和2個單位長度的速度向左運動,
分別以每秒3個單位長度和2個單位長度的速度向左運動,![]() 秒鐘過后,若點
秒鐘過后,若點![]() 與點B之間的距離表示為
與點B之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,則
,則![]() = ,
= , ![]() = (用含
= (用含![]() 的代數式表示);
的代數式表示);
(4)請問:AB+BC的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種流感病毒,有一人患了這種流感,在每輪傳染中一人將平均傳給x人.
(1)求第一輪后患病的人數;(用含x的代數式表示)
(2)在進入第二輪傳染之前,有兩位患者被及時隔離并治愈,問第二輪傳染后總共是否會有21人患病的情況發生,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的三邊AB、BC、CA長分別是20、30、40,其三條角平分線將△ABC分為三個三角形,則S△ABO︰S△BCO︰S△CAO等于( )

A. 1︰1︰1
B. 1︰2︰3
C. 2︰3︰4
D. 3︰4︰5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)在數軸上表示下列各數,并用“<”號把它們連接.
3, -1, 0, -2.5, 1.5, 2![]()
(2)快遞員要從物流中心出發送貨,已知甲住戶在物流中心的東邊 2km 處,乙住戶在甲住戶的西邊 3km 處,丙住戶在物流中心的西邊 1.5km 處,請建立數軸表示物流中心、甲住戶、乙住戶、丙住戶的位置關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍,設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
①求y關于x的函數關系式;
②該商店購進A型、B型電腦各多少臺,才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺.若商店保持兩種電腦的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺電腦銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD中,E是BC上一點,F是CD延長線上一點,![]() ,連接AE,AF,EF,G為EF中點,連接AG,DG.
,連接AE,AF,EF,G為EF中點,連接AG,DG.

(1)如圖1:若![]() ,
,![]() ,求DG;
,求DG;
(2)如圖2:延長GD至M,使![]() ,過M作MN∥FD交AF的延長線于N,連接NG,若
,過M作MN∥FD交AF的延長線于N,連接NG,若![]() .求證:
.求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com