
【題目】某中學八年級的籃球隊有10名隊員![]() 在“二分球”罰籃投球訓練中,這10名員各投籃50次的進球情況如下表:
在“二分球”罰籃投球訓練中,這10名員各投籃50次的進球情況如下表:
進球數 | 42 | 32 | 26 | 20 | 19 | 18 |
人數 | 1 | 1 | 2 | 1 | 2 | 3 |
針對這次訓練,請解答下列問題:
![]() 求這10名隊員進球數的平均數、中位數;
求這10名隊員進球數的平均數、中位數;
![]() 求這支球隊投籃命中率______;
求這支球隊投籃命中率______;
![]() 若隊員小亮“二分球”的投籃命中率為
若隊員小亮“二分球”的投籃命中率為![]() ,請你分析一下小亮在這支球隊中的投籃水平.
,請你分析一下小亮在這支球隊中的投籃水平.
![]() 投籃命中率
投籃命中率![]() 進球數
進球數![]() 投籃次數
投籃次數![]()
 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF折疊,使點B落在邊AD上的點B′處,點A落在點A′處;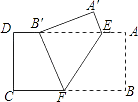
(1)求證:B′E=BF;
(2)設AE=a,AB=b,BF=c,試猜想a,b,c之間的一種關系,并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】填表:
相反數等于它本身 | 絕對值等于它本身 | 倒數等于它本身 | 平方等于它本身 | 立方等于它本身 | 平方根等于它本身 | 算術平方根等于它本身 | 立方根等于它本身 | 最大的負整數 | 絕對值最小的數 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學初三年級的同學參加了一項節能的社會調查活動,為了了解家庭用電的情況,他們隨即調查了某地50個家庭一年中生活用電的電費支出情況,并繪制了如下不完整的頻數分布表和頻數分布直方圖(費用取整數,單位:元).
分組/元 | 頻數 | 頻率 |
1000<x<1200 | 3 | 0.060 |
1200<x<1400 | 12 | 0.240 |
1400<x<1600 | 18 | 0.360 |
1600<x<1800 | a | 0.200 |
1800<x<2000 | 5 | b |
2000<x<2200 | 2 | 0.040 |
合計 | 50 | 1.000 |

請你根據以上提供的信息,解答下列問題:
(1)補全頻數分布表a= , b= , 和頻數分布直方圖;
(2)這50個家庭電費支出的中位數落在哪個組內?
(3)若該地區有3萬個家庭,請你估計該地區有多少個一年電費支出低于1400元的家庭?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙上的每個小方格都是邊長為1的正方形,我們把以格點間連線為邊的三角形稱為“格點三角形”,圖中的△ABC就是格點三角形.在建立平面直角坐標系后,點B的坐標為(﹣2,﹣1).
(1)把△ABC向左平移4格后得到△A1B1C1,畫出△A1B 1C1并寫出點A1的坐標;
(2)把△ABC繞點C按順時針旋轉90°后得到△A2B2C,畫出△A2B2C的圖形并寫出點A2的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一件工程甲獨做50天可完,乙獨做75天可完,現在兩個人合作,但是中途乙因事離開幾天,從開工后40天把這件工程做完,則乙中途離開了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中數學 來源: 題型:
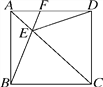
【題目】在正方形ABCD中,AC為對角線,點E為AC上一點,連接EB,ED.
(1)求證:△BEC≌△DEC;
(2)延長BE交AD于點F,當∠BED=120°時,求∠EFD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B、E分別在直線AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以證明
∠A=∠F.請完成下面證明過程中的各項“填空”
證明:∵∠AGB=∠EHF(已知)
∠AGB= (對頂角相等)
∴∠EHF=∠DGF(等量代換)
∴ ∥EC(理由: )
∴∠ =∠DBA(兩直線平行,同位角相等)
又∵∠C=∠D,∴∠DBA= (等量代換)
∴DF∥ (內錯角相等,兩直線平行)
∴∠A=∠F(理由: )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AB=4,AC=6,點D、E分別是BC.AD的中點,AF∥BC交CE的延長線于F.則四邊形AFBD的面積為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com