
【題目】如圖,甲樓AB高20 m,乙樓CD高10 m,兩棟樓之間的水平距離BD=20 m,小麗在乙樓樓頂C處觀測電視塔塔頂E,測得仰角為45°,求電視塔的高度EF.
(參考數據:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.4,結果保留整數)
≈1.4,結果保留整數)
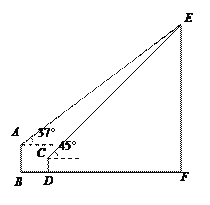
【答案】電視塔的高度為110米.
【解析】分析:首先分析題意,根據題意構造直角三角形,分別過點A,C作AM⊥EF,CN⊥EF垂足分別為M、N,在Rt△ECN和Rt△AEM中,借助三角函數解出AM、 CN的值,進而求出電視塔的高度.
詳解:如圖,分別過點A,C作AM⊥EF,CN⊥EF垂足分別為M、N.
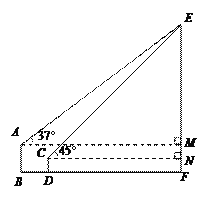
∴MF=AB=20,NF=CD=10.
設EF=x m,則EN=(x―10) m,EM=(x―20) m.
在Rt△ECN中,∠ECN=45°,
∵tan45°=![]() ,
,
∴CN=![]() =
=![]() .
.
在Rt△AEM中,∠EAM=37°,
∵ tan37°=![]() ,
,
∴AM=![]() =
=![]() .
.
又 AM―CN=BD,
∴![]() ―
―![]() =20.
=20.
∴x≈110.
答:電視塔的高度為110米.


科目:初中數學 來源: 題型:
【題目】如圖 ,已知△ ABC 中,點 D 、E 是 BC 邊上兩點,且 ADAE ,BAECAD 90 ,
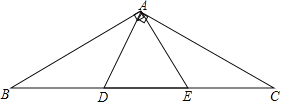
(1)試說明△ABE 與△ACD 全等的理由;
(2)如果 ADBD ,試判斷△ADE 的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
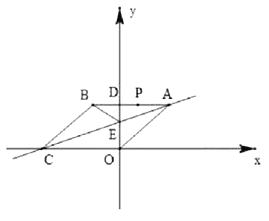
【題目】如圖,在平面直角坐標系中,點![]() 是原點,四邊形
是原點,四邊形![]() 是菱形,點
是菱形,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在
在![]() 軸的負半軸上,直線
軸的負半軸上,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() 與
與![]() 軸交于點
軸交于點![]() 。
。
(1)求直線![]() 的解析式;
的解析式;
(2)動點![]() 從點
從點![]() 出發,沿折線
出發,沿折線![]() 方向以1個單位/秒的速度向終點
方向以1個單位/秒的速度向終點![]() 勻速運動,設
勻速運動,設![]() 的面積為
的面積為![]() ,點
,點![]() 的運動時間為
的運動時間為![]() 秒,求
秒,求![]() 與
與![]() 之間的函數關系式。
之間的函數關系式。
查看答案和解析>>
科目:初中數學 來源: 題型:
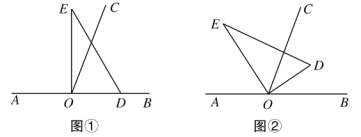
【題目】如圖,以直線AB上一點O為端點作射線OC,使∠BOC=70°,將一個直角三角板的直角頂點放在點O處(∠DOE=90°).
(1)如圖①,若直角三角板DOE的一邊OD放在射線OB上,則∠COE= °;
(2)如圖②,將直角三角板DOE繞點O轉動,若OD恰好平分∠BOC,求∠AOE的度數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】□ABCD中,∠A=60°,點E、F分別在邊AD、DC上,DE=DF,且∠EBF=60°.若AE=2,FC=3,則EF的長度為( )
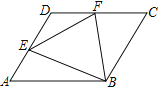
A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,∠C=90°,以AB為直徑的⊙O交AD于點E,CD=ED,連接BD交⊙O于點F.
(1)求證:BC與⊙O相切;
(2)若BD=10,AB=13,求AE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明在上學的路上要經過多個路口,每個路口都設有紅、黃、綠三種信號燈,假設在各路口遇到信號燈是相互獨立的.
(1).如果有2個路口,求小明在上學路上到第二個路口時第一次遇到紅燈的概率.(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
(2).如果有n個路口,則小明在每個路口都沒有遇到紅燈的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若將邊長為 a 、b 的正方形 ABCD 按圖 ① 中的比例進行分割,可以拼成一個長方形A1 B1C1D1 不重疊、無縫隙),如圖②所示.
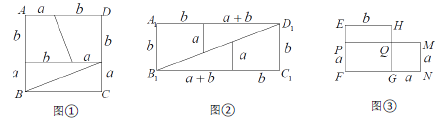
(1)根據圖①可以拼成圖②的面積關系,請寫出 a 、b 之間存在的關系式;
(2)已知圖③中,四邊形 QMNG 與四邊形EFGH 分別是以 a 、b 長為邊的正方形與圖①中的 a 、b 相同),在圖 3 已有的四邊形中,面積相等的四邊形有幾組?請分別寫出.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在黑板上出了一道解方程的題:![]() ,小明馬上舉起了手,要求到黑板上去做,他是這樣做的:4(2x﹣1)=1﹣3(x+2),①
,小明馬上舉起了手,要求到黑板上去做,他是這樣做的:4(2x﹣1)=1﹣3(x+2),①
8x﹣4=1﹣3x﹣6,②
8x+3x=1﹣6+4,③
11x=﹣1,④
x=﹣![]() .⑤
.⑤
老師說:小明解一元一次方程的一般步驟都掌握了,但解題時有一步做錯了.請你指出他錯在第 步(填編號),然后再細心地解下面的方程,相信你一定能做對.
(1)5(x+8)=6(2x﹣7)+5;
(2)![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com