
【題目】對(duì)數(shù)軸上的點(diǎn)![]() 進(jìn)行如下操作:先把點(diǎn)
進(jìn)行如下操作:先把點(diǎn)![]() 表示的數(shù)乘以
表示的數(shù)乘以![]() ,再把所得數(shù)對(duì)應(yīng)的點(diǎn)沿?cái)?shù)軸向右平移
,再把所得數(shù)對(duì)應(yīng)的點(diǎn)沿?cái)?shù)軸向右平移![]() 個(gè)單位長(zhǎng)度,得到點(diǎn)
個(gè)單位長(zhǎng)度,得到點(diǎn)![]() .稱(chēng)這樣的操作為點(diǎn)
.稱(chēng)這樣的操作為點(diǎn)![]() 的“倍移”,對(duì)數(shù)軸上的點(diǎn)
的“倍移”,對(duì)數(shù)軸上的點(diǎn)![]() ,
,![]() ,
, ![]() ,
,![]() 進(jìn)行“倍移”操作得到的點(diǎn)分別為
進(jìn)行“倍移”操作得到的點(diǎn)分別為![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)當(dāng)![]() ,
,![]() 時(shí),
時(shí),
①若點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,則它的對(duì)應(yīng)點(diǎn)
,則它的對(duì)應(yīng)點(diǎn)![]() 表示的數(shù)為 .若點(diǎn)
表示的數(shù)為 .若點(diǎn)![]() 表示的數(shù)是
表示的數(shù)是![]() ,則點(diǎn)
,則點(diǎn)![]() 表示的數(shù)為 ; ②數(shù)軸上的點(diǎn)
表示的數(shù)為 ; ②數(shù)軸上的點(diǎn)![]() 表示的數(shù)為1,若
表示的數(shù)為1,若![]() ,則點(diǎn)
,則點(diǎn)![]() 表示的數(shù)為 ;
表示的數(shù)為 ;
(2)當(dāng)![]() 時(shí),若點(diǎn)
時(shí),若點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,則
,則![]() 的值為 ;
的值為 ;
(3)若線段![]() ,請(qǐng)寫(xiě)出你能由此得到的結(jié)論.
,請(qǐng)寫(xiě)出你能由此得到的結(jié)論.
【答案】(1)① ![]() ;
;![]() ; ②
; ② ![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 等
等
【解析】
(1)①根據(jù)題目規(guī)定以及數(shù)軸上的數(shù)向右平移用加法計(jì)算即可求出點(diǎn)![]() ,設(shè)點(diǎn)B表示的數(shù)為a,根據(jù)題意列出方程求解即可得到點(diǎn)B表示的數(shù);
,設(shè)點(diǎn)B表示的數(shù)為a,根據(jù)題意列出方程求解即可得到點(diǎn)B表示的數(shù);
②設(shè)點(diǎn)C表示的數(shù)為b,根據(jù)“倍移”規(guī)律得到點(diǎn)![]() 表示的數(shù)為
表示的數(shù)為![]() ,從而可表示出CM,
,從而可表示出CM,![]() M,根據(jù)
M,根據(jù)![]() 列方程求解即可得到答案;
列方程求解即可得到答案;
(2)根據(jù)“倍移”規(guī)律列方程求解即可;
(3)設(shè)A點(diǎn)表示的數(shù)為x,B點(diǎn)表示的數(shù)為y,則![]() 表示的數(shù)為mx+n,
表示的數(shù)為mx+n,![]() 表示的數(shù)為my+n,
表示的數(shù)為my+n,
根據(jù)![]() 列方程求解即可.
列方程求解即可.
(1)①點(diǎn)A′:![]() ;
;
設(shè)點(diǎn)B表示的數(shù)為a,根據(jù)題意得:![]()
解得,a=4,
∴點(diǎn)![]() 表示的數(shù)為:4;
表示的數(shù)為:4;
②設(shè)點(diǎn)C表示的數(shù)為b,
所以,點(diǎn)![]() 表示的數(shù)為:
表示的數(shù)為:![]() ,
,
∵點(diǎn)![]() 表示的數(shù)為1,
表示的數(shù)為1,
∴CM=|b-1|,![]() ,
,
∵![]() ,
,
∴|b-1|=3|![]() |
|
∴![]() ,
,
解得:b=-2或b=![]() ,
,
故C點(diǎn)表示的數(shù)為:b=-2或b=![]() ;
;
(2)根據(jù)題意得,![]() ,
,
解得,m=-4;
(3)設(shè)A點(diǎn)表示的數(shù)為x,B點(diǎn)表示的數(shù)為y,則![]() 表示的數(shù)為mx+n,
表示的數(shù)為mx+n,![]() 表示的數(shù)為my+n,
表示的數(shù)為my+n,
∴AB=|x-y|,![]()
∵![]()
∴![]()
∴![]() ,
,
∴m=±2.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如果關(guān)于![]() 的不等式組
的不等式組![]() 的整數(shù)解僅有
的整數(shù)解僅有![]() ,
,![]() ,那么適合這個(gè)不等式組的整數(shù)
,那么適合這個(gè)不等式組的整數(shù)![]() ,
,![]() 組成的有序數(shù)對(duì)
組成的有序數(shù)對(duì)![]() 共有_______個(gè);如果關(guān)于
共有_______個(gè);如果關(guān)于![]() 的不等式組
的不等式組![]() (其中
(其中![]() ,
,![]() 為正整數(shù))的整數(shù)解僅有
為正整數(shù))的整數(shù)解僅有![]() ,那么適合這個(gè)不等式組的整數(shù)
,那么適合這個(gè)不等式組的整數(shù)![]() ,
,![]() 組成的有序數(shù)對(duì)
組成的有序數(shù)對(duì)![]() 共有______個(gè).(請(qǐng)用含
共有______個(gè).(請(qǐng)用含![]() 、
、![]() 的代數(shù)式表示)
的代數(shù)式表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BE=4,CD=6,則DE的長(zhǎng)為________.
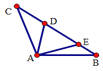
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在菱形ABCD中,對(duì)角線AC、BD相交于點(diǎn)O,過(guò)點(diǎn)D作對(duì)角線BD的垂線交BA的延長(zhǎng)線于點(diǎn)E.
(1)證明:四邊形ACDE是平行四邊形;
(2)若AC=8,BD=6,求平行四邊形ACDE的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小明在學(xué)習(xí)二次根式后,發(fā)現(xiàn)一些含根號(hào)的式子可以寫(xiě)成另一個(gè)式子的平方,如:3+2![]() ,善于思考的小明進(jìn)行了以下探索:
,善于思考的小明進(jìn)行了以下探索:
設(shè)a+b![]() (其中a、b、m、n均為整數(shù)),
(其中a、b、m、n均為整數(shù)),
則有:a+b![]() ,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類(lèi)似a+b
,∴a=m2+2n2,b=2mn,這樣小明就找到了一種把類(lèi)似a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請(qǐng)你仿照小明的方法探索并解決下列問(wèn)題:
(1)當(dāng)a、b、m、n均為正整數(shù)時(shí),若a+b![]() ,用含m、n的式子分別表示a、b得:a= ,b= ;
,用含m、n的式子分別表示a、b得:a= ,b= ;
(2)利用所探索的結(jié)論,用完全平方式表示出:7+4![]() = .
= .
(3)請(qǐng)化簡(jiǎn):![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2017南寧,第26題,10分)如圖,已知拋物線![]() 與坐標(biāo)軸交于A,B,C三點(diǎn),其中C(0,3),∠BAC的平分線AE交y軸于點(diǎn)D,交BC于點(diǎn)E,過(guò)點(diǎn)D的直線l與射線AC,AB分別交于點(diǎn)M,N.
與坐標(biāo)軸交于A,B,C三點(diǎn),其中C(0,3),∠BAC的平分線AE交y軸于點(diǎn)D,交BC于點(diǎn)E,過(guò)點(diǎn)D的直線l與射線AC,AB分別交于點(diǎn)M,N.
(1)直接寫(xiě)出a的值、點(diǎn)A的坐標(biāo)及拋物線的對(duì)稱(chēng)軸;
(2)點(diǎn)P為拋物線的對(duì)稱(chēng)軸上一動(dòng)點(diǎn),若△PAD為等腰三角形,求出點(diǎn)P的坐標(biāo);
(3)證明:當(dāng)直線l繞點(diǎn)D旋轉(zhuǎn)時(shí),![]() 均為定值,并求出該定值.
均為定值,并求出該定值.
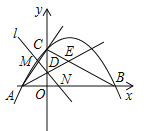
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1是一種折疊椅,忽略其支架等的寬度,得到它的側(cè)面簡(jiǎn)化結(jié)構(gòu)圖(圖2),支架與坐板均用線段表示.若座板CD平行于地面,前支撐架AB與后支撐架OF分別與CD交于點(diǎn)E、D,ED= 15㎝,OD=20㎝,DF=40㎝,∠ODC=60°,∠AED=50°.
(1)求兩支架著地點(diǎn)B、F之間的距離;
(2)若A、D兩點(diǎn)所在的直線正好與地面垂直,求椅子的高度(結(jié)果取整數(shù)).
(參考數(shù)據(jù): ![]()
![]() ;可使用科學(xué)計(jì)算器.)
;可使用科學(xué)計(jì)算器.)
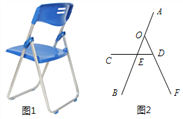
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,△DBE和△ABC都是等腰直角三角形,D,E兩點(diǎn)分別在AB,BC上,∠B=90°.將△DBE繞點(diǎn)B順時(shí)針旋轉(zhuǎn),得到圖2.
(1)在圖2中,求證:AD=CE;
(2)設(shè)AB= ![]() ,BD=
,BD= ![]() ,且當(dāng)A、D、E三點(diǎn)在同一直線上時(shí),∠EAC=30°,請(qǐng)利用備用圖畫(huà)出此情況下的圖形,并求旋轉(zhuǎn)的角度和
,且當(dāng)A、D、E三點(diǎn)在同一直線上時(shí),∠EAC=30°,請(qǐng)利用備用圖畫(huà)出此情況下的圖形,并求旋轉(zhuǎn)的角度和![]() 的值.
的值.
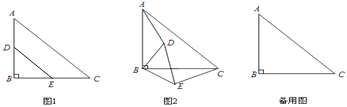
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,一次函數(shù)y1=x+2與反比例函數(shù)y2=![]() (x>0)的圖象交于點(diǎn)A(a,5)
(x>0)的圖象交于點(diǎn)A(a,5)
(1)確定反比例函數(shù)的表達(dá)式;
(2)結(jié)合圖象,直接寫(xiě)出x為何值時(shí),y1<y2
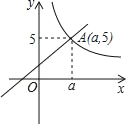
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com