
【題目】平面直角坐標系xOy中,點A、B分別在函數y1=![]() (x>0)與y2=
(x>0)與y2=![]() (x<0)的圖象上,A、B的橫坐標分別為a、b.
(x<0)的圖象上,A、B的橫坐標分別為a、b.
(1)若AB∥x軸,求△OAB的面積;
(2)若△OAB是以AB為底邊的等腰三角形,且a+b![]() 0,求ab的值;
0,求ab的值;
(3)作邊長為3的正方形ACDE,使AC∥x軸,點D在點A的左上方,那么,對大于或等于4的任意實數a,CD邊與函數y1=![]() (x>0)的圖象都有交點,請說明理由.
(x>0)的圖象都有交點,請說明理由.

【答案】(1)S△OAB=4;(2)ab=﹣4;(3)見解析.
【解析】
(1)如圖1,AB交y軸于C,由于AB∥x軸,根據k的幾何意義得到S△OAC=2,S△OBC=2,所以S△OAB=S△OAC+S△OBC=4;
(2)根據函數圖象上點的坐標特征得A、B的縱坐標分別為![]() ,根據兩點間的距離公式得到
,根據兩點間的距離公式得到![]() ,則利用等腰三角形的性質得到a2+(
,則利用等腰三角形的性質得到a2+(![]() )2=b2+(﹣
)2=b2+(﹣![]() )2,變形得到(a+b)(a﹣b)(1﹣
)2,變形得到(a+b)(a﹣b)(1﹣![]() )=0,由于a+b≠0,a>0,b<0,所以1﹣
)=0,由于a+b≠0,a>0,b<0,所以1﹣![]() =0,易得ab=﹣4;
=0,易得ab=﹣4;
(3)由于a≥4,AC=3,則可判斷直線CD在y軸的右側,直線CD與函數y1=![]() (x>0)的圖象一定有交點,設直線CD與函數y1=
(x>0)的圖象一定有交點,設直線CD與函數y1=![]() (x>0)的圖象交點為F,由于A點坐標為(a,
(x>0)的圖象交點為F,由于A點坐標為(a,![]() ),正方形ACDE的邊長為3,則得到C點坐標為(a﹣3,
),正方形ACDE的邊長為3,則得到C點坐標為(a﹣3,![]() ),F點的坐標為(a﹣3,
),F點的坐標為(a﹣3,![]() ),所以FC=
),所以FC=![]() ,然后比較FC與3的大小,由于3﹣FC=3﹣
,然后比較FC與3的大小,由于3﹣FC=3﹣![]() ,而a≥4,所以3﹣FC≥0,于是可判斷點F在線段DC上.
,而a≥4,所以3﹣FC≥0,于是可判斷點F在線段DC上.
解:(1)如圖,AB交y軸于P,
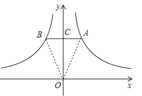
∵AB∥x軸,
∴S△OAC=![]() ×|4|=2,S△OBC=
×|4|=2,S△OBC=![]() ×|﹣4|=2,
×|﹣4|=2,
∴S△OAB=S△OAC+S△OBC=4;
(2)∵A、B的橫坐標分別為a、b,
∴OA2=a2+(![]() )2,OB2=b2+(﹣
)2,OB2=b2+(﹣![]() )2,
)2,
∵△OAB是以AB為底邊的等腰三角形,
∴OA=OB,
∴a2+(![]() )2=b2+(﹣
)2=b2+(﹣![]() )2
)2
∴(a+b)(a﹣b)(1﹣![]() )=0,
)=0,
∵a+b≠0,a>0,b<0,
∴1﹣![]() =0,
=0,
∴ab=﹣4
(3)∵a≥4,而AC=3,
∴直線CD在y軸的右側,直線CD與函數y1=![]() (x>0)的圖象一定有交點,
(x>0)的圖象一定有交點,
設直線CD與函數y1=![]() (x>0)的圖象交點為F,如圖,
(x>0)的圖象交點為F,如圖,
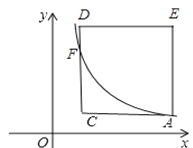
∵A點坐標為(a,![]() ),正方形ACDE的邊長為3,
),正方形ACDE的邊長為3,
∴C點坐標為(a﹣3,![]() ),
),
∴F點的坐標為(a﹣3,![]() ),
),
∴FC=![]() ﹣
﹣![]()
∵3﹣FC=3﹣![]() ,
,
而a≥4,
∴3﹣FC≥0,即FC≤3,
∵CD=3,
∴點F在線段DC上,
即對大于或等于4的任意實數a,CD邊與函數y1=![]() (x>0)的圖象都有交點
(x>0)的圖象都有交點


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
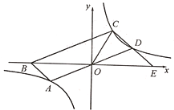
【題目】如圖,在平面直角坐標系中,平行四邊形ABCD的邊AD經過O點,A、C、D三點都在反比例函數![]() 的圖像上,B點在
的圖像上,B點在![]() 軸的負半軸上,延長CD交
軸的負半軸上,延長CD交![]() 軸于點E,連接CO.
軸于點E,連接CO.
若C(1,2),D(2,1),則![]() 為_______.
為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】你吃過拉面嗎?實際上在做拉面的過程中就滲透著數學知識:一定體積的面團做成拉面,面條的總長度y(m)四面條的粗細(橫截面積)S(mm2)的反比例函數,其圖象如圖所示.
(1)寫出y與S的函數關系式;
(2)求當面條粗1.6 mm2時,面條的總長度是多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
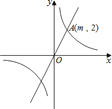
【題目】如圖,在平面直角坐標系xOy中,正比例函數y=kx的圖象與反比例函數![]() 的圖象有一個交點A(m,2).
的圖象有一個交點A(m,2).
(1)求m的值及正比例函數y=kx的解析式;
(2)試判斷點B(2,3)是否在正比例函數圖象上,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
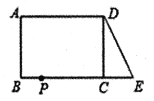
【題目】已知:如圖,在長方形![]() 中,
中,![]() ,
,![]() .延長
.延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,動點
,動點![]() 從點
從點![]() 出發,以每秒2個單位的速度沿
出發,以每秒2個單位的速度沿![]() 向終點
向終點![]() 運動,設點
運動,設點![]() 的運動時間為
的運動時間為![]() 秒,當
秒,當![]() 的值為___________時,
的值為___________時,![]() 和
和![]() 全等.
全等.
查看答案和解析>>
科目:初中數學 來源: 題型:
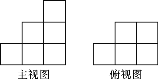
【題目】由一些大小相同的小正方體組成的簡單幾何體的主視圖和俯視圖如圖29-29所示.
(1)請你畫出這個幾何體的一種左視圖.
(2)若組成這個幾何體的小正方體的塊數為n,請你寫出n的所有可能值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com