
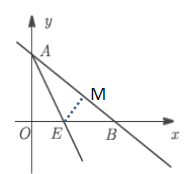
【題目】如圖,已知一次函數![]() 的圖象與坐標軸分別交于A、B點,AE平分
的圖象與坐標軸分別交于A、B點,AE平分![]() ,交
,交![]() 軸于點E.
軸于點E.

(1)直接寫出點A和點B的坐標.
(2)求直線AE的表達式.
(3)過點B作BF![]() AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交
AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交![]() 軸于點C,判斷四邊形ACFD的形狀并說明理由,求四邊形ACFD的面積.
軸于點C,判斷四邊形ACFD的形狀并說明理由,求四邊形ACFD的面積.
【答案】(1)A(0,6),B(8,0);(2)y=2x+6;(3)四邊形ACFD是菱形,證明見解析;S四邊形ACFD=20
【解析】
(1)一次函數![]() ,令x=0求出y值,可得A點坐標,令y=0,求出x值,可得B點坐標,此題得解;
,令x=0求出y值,可得A點坐標,令y=0,求出x值,可得B點坐標,此題得解;
(2)已知A,B點坐標,結合勾股定理可求出AB的長度,再利用角平分線的性質即可求出點E的坐標,根據點A、E的坐標利用待定系數法即可求出直線AE的表達式;
(3)過點B作BF![]() AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交
AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交![]() 軸于點C,連接CD交AF于點G,可得四邊形ACFD是平行四邊形,證明AD=DF,即可得到四邊形ACFD是菱形,證明△AOE∽△BFE,即可得到
軸于點C,連接CD交AF于點G,可得四邊形ACFD是平行四邊形,證明AD=DF,即可得到四邊形ACFD是菱形,證明△AOE∽△BFE,即可得到![]() ,
,![]() ,求得BF和EF,進而求得四邊形ACFD的面積.
,求得BF和EF,進而求得四邊形ACFD的面積.
(1)∵![]()
當x=0時,y=6
∴A(0,6)
當y=0時,![]()
解得x=8
∴B(8,0)
∴A(0,6),B(8,0)
(2)過點E作EM⊥AB于D
∴OA=6,OB=8,
∴AB=![]()
∵AE平分∠BAO,交x軸于點E
∴OE=ME
∴![]()
∴![]()
∴OE=![]() BE
BE
∵OE+BE=OB=8
∴OE=3,BE=5
∴點E的坐標為(3,0)
設直線AE的表達式為y=kx+b
將A(0,6)、E(3,0)代入y=kx+b
![]()
解得:![]()
∴直線AE的表達式為y=2x+6
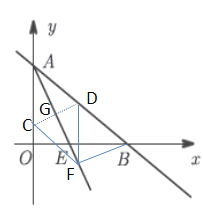
(3)過點B作BF![]() AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交
AE于點F,過點F分別作FD//OA交AB于點D,FC//AB交![]() 軸于點C,連接CD交AF于點G
軸于點C,連接CD交AF于點G
∵FD//OA,FC//AB
∴四邊形ACFD是平行四邊形
∴∠CAF=∠AFD
∵∠CAF=∠FAD
∴∠AFD=∠FAD
∴AD=DF
∴四邊形ACFD是菱形
∵∠AOE=∠BFE=90°,∠AEO=∠BEF
∴△AOE∽△BFE
∴![]()
∵OE=3,OA=6
∴AE=![]()
∴![]()
∴BF=![]()
∵四邊形ACFD是菱形
∴DG⊥AF,AG=GF
∴DG=![]() BF=
BF=![]()
∵![]()
∴![]()
∴EF=![]()
∴AF=AE+EF=![]()
S四邊形ACFD=AF×DG=![]()
故答案為:四邊形ACFD是菱形,證明見解析;S四邊形ACFD=20


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】由于受到手機更新換代的影響,某手機店經銷![]() 型號手機四月售價比三月每臺降價500元.如果賣出相同數量的
型號手機四月售價比三月每臺降價500元.如果賣出相同數量的![]() 型號手機,那么三月銷售額為9萬元,四月銷售額只有8萬元.
型號手機,那么三月銷售額為9萬元,四月銷售額只有8萬元.
(1)三月![]() 型號手機每臺售價為多少元?
型號手機每臺售價為多少元?
(2)為了提高利潤,該店計劃五月購進![]() 型號手機銷售,已知
型號手機銷售,已知![]() 型號每臺進價為3500元,
型號每臺進價為3500元,![]() 型號每臺進價為4000元,預計用不多于7.6萬元且不少于7.4萬元的資金購進這兩種手機共20臺,請問有幾種進貨方案?
型號每臺進價為4000元,預計用不多于7.6萬元且不少于7.4萬元的資金購進這兩種手機共20臺,請問有幾種進貨方案?
(3)該店計劃六月對![]() 型號的尾貨進行銷售,決定在四月售價基礎上每售出一臺
型號的尾貨進行銷售,決定在四月售價基礎上每售出一臺![]() 型號手機再返還顧客現金
型號手機再返還顧客現金![]() 元,而
元,而![]() 型號按銷售價4400元銷售,如要使(2)中所有方案獲利相同,
型號按銷售價4400元銷售,如要使(2)中所有方案獲利相同,![]() 應取何值?
應取何值?
查看答案和解析>>
科目:初中數學 來源: 題型:
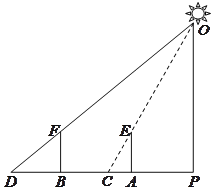
【題目】高高地路燈掛在路邊的上方,高傲而明亮,小明拿著一根![]() 米長的竹竿,想量一量路燈的高度,直接量是不可能的,于是,他走到路燈旁的一個地方,豎起竹竿,這時,他量了一下竹竿的影長正好是
米長的竹竿,想量一量路燈的高度,直接量是不可能的,于是,他走到路燈旁的一個地方,豎起竹竿,這時,他量了一下竹竿的影長正好是![]() 米,他沿著影子的方向走,向遠處走出兩根竹竿的長度(即
米,他沿著影子的方向走,向遠處走出兩根竹竿的長度(即![]() 米),他又豎起竹竿,這時竹竿的影長正好是一根竹竿的長度(即
米),他又豎起竹竿,這時竹竿的影長正好是一根竹竿的長度(即![]() 米).此時,小明抬頭瞧瞧路燈,若有所思地說:“噢,原來路燈有
米).此時,小明抬頭瞧瞧路燈,若有所思地說:“噢,原來路燈有![]() 米高呀!”(如圖所示)同學們,你覺得小明的判斷對嗎?
米高呀!”(如圖所示)同學們,你覺得小明的判斷對嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
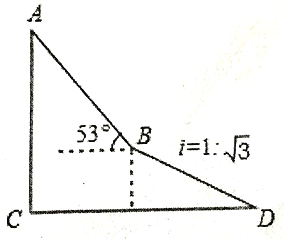
【題目】如圖,為了測量出樓房AC的高度,從距離樓底C處60![]() 米的點D(點D與樓底C在同一水平上)出發,沿斜面坡度為i=l:
米的點D(點D與樓底C在同一水平上)出發,沿斜面坡度為i=l: ![]() 的斜坡DB前進30米到達點B,在點B處測得樓頂A的仰角為53
的斜坡DB前進30米到達點B,在點B處測得樓頂A的仰角為53![]() ,求樓房AC的高度(參考數據:sin53
,求樓房AC的高度(參考數據:sin53![]() =
=![]() , cos53
, cos53![]() =
=![]() , tan53
, tan53![]() =
=![]() ,
, ![]() ≈1.732,結果精確到0.1米)
≈1.732,結果精確到0.1米)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知平面直角坐標系內A(2a-1,4),B(-3,3b+1),A、B兩點關于y軸對稱。
(1)求A、B的坐標
(2)動點P、Q分別從A點、B點同時出發,沿直線AB向右運動,同向而行,P點的速度是每秒2個單位長度,Q點的速度是每秒4個單位長度,設P、Q的運動時間為t秒,當0<t<3時.
①請用含t的代數式表示三角形OPQ的面積S,
②在平面直角坐標系中存在一點M,點M的橫縱坐標相等,且滿足![]() ,求出點M的坐標,并求出當
,求出點M的坐標,并求出當![]() =15時,三角形OPQ的面積.
=15時,三角形OPQ的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB∶BC∶CA=3∶4∶5,且周長為36cm,點P從點A開始沿AB邊向B點以每秒1cm的速度移動;點Q從點B開始沿BC邊向點C以每秒2cm的速度移動,如果點P,Q同時出發,那么過3s時,△BPQ的面積為多少?
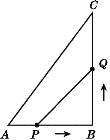
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學準備購買筆和本子送給農村希望小學的同學,在市場上了解到某種本子的單價比某種筆的單價少4元,且用30元買這種本子的數量與用50元買這種筆的數量相同.
(1)求這種筆和本子的單價;
(2)該同學打算用自己的100元壓歲錢購買這種筆和本子,計劃100元剛好用完,并且筆和本子都買,請列出所有購買方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com