
【題目】如圖,點A、B是數軸上的兩個點,它們分別表示的數是![]() 和1. 點A與點B之間的距離表示為AB.
和1. 點A與點B之間的距離表示為AB.
(1)AB= .
(2)點P是數軸上A點右側的一個動點,它表示的數是![]() ,滿足
,滿足![]() ,求
,求![]() 的值.
的值.
(3)點C為6. 若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和5個單位長度的速度向右運動.請問:![]() 的值是否隨著運動時間t(秒)的變化而改變? 若變化,請說明理由;若不變,請求其值.
的值是否隨著運動時間t(秒)的變化而改變? 若變化,請說明理由;若不變,請求其值.
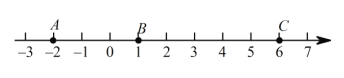
【答案】(1)3.(2)存在.x的值為3.(3)不變,為2.
【解析】
(1)根據非負數的性質和數軸上兩點間距離即可求解;
(2)分兩種情況討論,根據數軸上兩點間的距離公式列方程即可求解;
(3)先確定運動t秒后,A、B、C三點對應的數,再根據數軸上兩點間的距離公式列方程即可求解.
解:(1)∵點A、B是數軸上的兩個點,它們分別表示的數是![]() 和1
和1
∴A,B兩點之間的距離是1-(-2)=3.
故答案為3.
(2)存在.理由如下:
①若P點在A、B之間,
x+2+1-x=7,此方程不成立;
②若P點在B點右側,
x+2+x-1=7,解得x=3.
答:存在.x的值為3.
(3)![]() 的值不隨運動時間t(秒)的變化而改變,為定值,是2.理由如下:
的值不隨運動時間t(秒)的變化而改變,為定值,是2.理由如下:
運動t秒后,A點表示的數為-2-t,B點表示的數為1+2t,C點表示的數為6+5t.
所以AB=1+2t-(-2-t)=3+3t.
BC=6+5t-(1+2t)=5+3t.
所以BC-AB=5+3t-3-3t=2.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,將一副直角三角板放在同一條直線AB上,其中∠ONM=30°,∠OCD=45°.
(1)將圖①中的三角板OMN沿BA方向平移至圖②的位置,MN與CD相交于點E,求∠CEN的度數;
(2)將圖①中的三角板OMN繞點O按逆時針方向旋轉,使∠BON=30°,如圖③,MN與CD相交于點E,求∠CEN的度數;
(3)將圖①中的三角尺COD繞點O按每秒15°的速度沿順時針防線旋轉一周,在旋轉過程中,在第幾秒時,MN恰好與CD平行;第幾秒時,MN恰好與直線CD垂直.

查看答案和解析>>
科目:初中數學 來源: 題型:
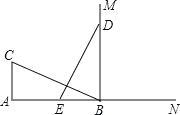
【題目】如圖,CA⊥AB,垂足為 A,AB=24,AC=12,射線 BM⊥AB,垂足為 B, 一動點 E 從 A點出發以 3 厘米/秒沿射線 AN 運動,點 D 為射線 BM 上一動點, 隨著 E 點運動而運動,且始終保持 ED=CB,當點 E 經過______秒時,△DEB 與△BCA 全等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”,為保護生態環境,A,B兩村準備各自清理所屬區域養魚網箱和捕魚網箱,每村參加清理人數及總開支如下表:
村莊 | 清理養魚網箱人數/人 | 清理捕魚網箱人數/人 | 總支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若兩村清理同類漁具的人均支出費用一樣,求清理養魚網箱和捕魚網箱的人均支出費用各是多少元;
(2)在人均支出費用不變的情況下,為節約開支,兩村準備抽調40人共同清理養魚網箱和捕魚網箱,要使總支出不超過102000元,且清理養魚網箱人數小于清理捕魚網箱人數,則有哪幾種分配清理人員方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
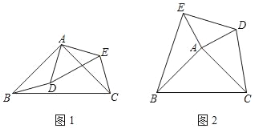
【題目】已知,等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°.
(1)如圖1,求證:DB=CE;
(2)如圖2.求證:S△ACD=S△ABE.
查看答案和解析>>
科目:初中數學 來源: 題型:
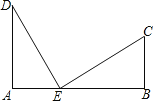
【題目】如圖,筆直的公路上A、B兩點相距25km,C、D為兩村莊,DA⊥AB于點A,CB⊥AB于點B,已知DA=15km,CB=10km,現在要在公路的AB段上建一個土特產品收購站E,使得C、D兩村到收購站E的距離相等,則收購站E應建在離A點多遠處?
查看答案和解析>>
科目:初中數學 來源: 題型:
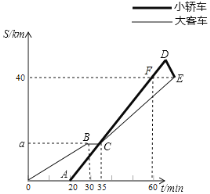
【題目】初二![]() 班同學從學校出發去某自然保護區研學旅行,一部分乘坐大客車先出發,余下的幾人20分鐘后乘坐小轎車沿同一路線出行
班同學從學校出發去某自然保護區研學旅行,一部分乘坐大客車先出發,余下的幾人20分鐘后乘坐小轎車沿同一路線出行![]() 大客車中途停車等候,小轎車趕上來之后,大客車以出發時速度的
大客車中途停車等候,小轎車趕上來之后,大客車以出發時速度的![]() 繼續行駛,小轎車保持原速度不變
繼續行駛,小轎車保持原速度不變![]() 小轎車司機因路線不熟錯過了景點入口,再原路提速返回,恰好與大客車同時到達景點入口
小轎車司機因路線不熟錯過了景點入口,再原路提速返回,恰好與大客車同時到達景點入口![]() 兩車距學校的路程
兩車距學校的路程![]() 單位:千米
單位:千米![]() 和行駛時間
和行駛時間![]() 單位:分鐘
單位:分鐘![]() 之間的函數關系如圖所示.
之間的函數關系如圖所示.
請結合圖象解決下面問題:
![]() 學校到景點的路程為______千米,大客車途中停留了______分鐘,
學校到景點的路程為______千米,大客車途中停留了______分鐘,![]() ______千米;
______千米;
![]() 在小轎車司機駛過景點入口時,大客車離景點入口還有多遠?
在小轎車司機駛過景點入口時,大客車離景點入口還有多遠?
![]() 若大客車一直以出發時的速度行駛,中途不再停車,那么小轎車折返后到達景點入口,需等待______分鐘,大客車才能到達景點入口.
若大客車一直以出發時的速度行駛,中途不再停車,那么小轎車折返后到達景點入口,需等待______分鐘,大客車才能到達景點入口.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】宜賓某商店決定購進A.B兩種紀念品.購進A種紀念品7件,B種紀念品2件和購進A種紀念品5件,B種紀念品6件均需80元.
(1)求購進A、B兩種紀念品每件各需多少元?
(2)若該商店決定購進這兩種紀念品共100件,考慮市場需求和資金周轉,用于購買這100件紀念品的資金不少于750元,但不超過764元,那么該商店共有幾種進貨方案?
(3)已知商家出售一件A種紀念品可獲利a元,出售一件B種紀念品可獲利(5﹣a)元,試問在(2)的條件下,商家采用哪種方案可獲利最多?(商家出售的紀念品均不低于成本價)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com