
【題目】對于二次函數![]() ,有下列說法:
,有下列說法:
①如果當x≤1時![]() 隨
隨![]() 的增大而減小,則m≥1;
的增大而減小,則m≥1;
②如果它的圖象與x軸的兩交點的距離是4,則![]() ;
;
③如果將它的圖象向左平移3個單位后的函數的最小值是-4,則m=-1;
④如果當x=1時的函數值與x=2013時的函數值相等,則當x=2014時的函數值為-3.
其中正確的說法是 .
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某市創建“綠色發展模范城市”,針對境內長江段兩種主要污染源:生活污水和沿江工廠污染物排放,分別用“生活污水集中處理”(下稱甲方案)和“沿江工廠轉型升級”(下稱乙方案)進行治理,若江水污染指數記為Q,沿江工廠用乙方案進行一次性治理(當年完工),從當年開始,所治理的每家工廠一年降低的Q值都以平均值n計算.第一年有40家工廠用乙方案治理,共使Q值降低了12.經過三年治理,境內長江水質明顯改善.
(1)求n的值;
(2)從第二年起,每年用乙方案新治理的工廠數量比上一年都增加相同的百分數m,三年來用乙方案治理的工廠數量共190家,求m的值,并計算第二年用乙方案新治理的工廠數量;
(3)該市生活污水用甲方案治理,從第二年起,每年因此降低的Q值比上一年都增加個相同的數值a.在(2)的情況下,第二年,用乙方案所治理的工廠合計降低的Q值與當年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于有理數a,b,定義兩種新運算“※”與“◎”,規定: a※b=a2+2ab,a◎b=|a+ b|-|a- b|,例如,2※(- 1)=22+2×2×(-1)=0,(- 2) ※3=|-2+3|-| - 2-3|= -4.![]() b c
b c
(1)計算(- 3) ※2的值;
(2)若a, b在數軸上的位置如圖所示,化簡a◎b;
![]()
(3)若(-2) ※x=2◎(- 4)+ 3x,求x的值:
(4)對于任意有理數m,n,請你定義一種新運算“★” ,使得(-3) ★5 = 4,直接寫出你定義的運算:m★n=_ (用含m,n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在同一水平面從左到右依次是大廈、別墅、小山、小彬為了測得小山的高度,在大廈的樓頂B處測得山頂C的俯角∠GBC=13°,在別墅的大門A點處測得大廈的樓頂B點的仰角∠BAO=35°,山坡AC的坡度i=1:2,OA=500米,則山C的垂直高度約為( )(參考數據:sin13°≈0.22,tan13°≈0.23,sin35°≈0.57)

A. 161.0 B. 116.4 C. 106.8 D. 76.2
查看答案和解析>>
科目:初中數學 來源: 題型:
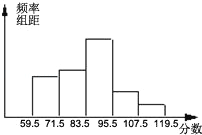
【題目】我市某區對參加市模擬考試的8000名學生的數學成績進行抽樣調查,抽取了部分學生的數學成績(分數為整數)進行統計,繪制成頻率分布直方圖.如下圖,已知從左到右五個小組的頻數是之比依次是6:7:11:4:2,第五小組的頻數是40.
(1)本次調查共抽取了多少名學生?
(2)若72分以上(含72分)為及格,96分以上(含96分)為優秀,那么抽取的學生中,及格的人數、優秀的人數各占所抽取的學生數的百分之多少?
(3)根據(2)的結論,該區所有參加市模擬考試的學生,及格人數、優秀人數各約是多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
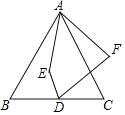
【題目】如圖,等邊△ABC中,AB=10,D為BC的中點,E為△ABC內一動點,DE=3,連接AE,將線段AE繞點A逆時針旋轉60°得AF,連接DF,求線段DF的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,鐵路MN和公路PQ在點O處交匯,∠QON=30°,公路PQ上A處距O點240米,如果火車行駛時,周圍200米以內會受到噪音的影響,那么火車在鐵路MN上沿ON方向以72千米/時的速度行駛時,求A處受噪音影響的時間。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com