Question

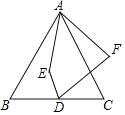
【題目】如圖，等邊△ABC中，AB=10，D為BC的中點，E為△ABC內一動點，DE=3，連接AE，將線段AE繞點A逆時針旋轉60°得AF，連接DF，求線段DF的最小值.

Answer 1

【答案】5-3

【解析】

以ED為邊作等邊△DEG，連接AD，EF，AG，由等邊三角形的性質和勾股定理可求AD=5，由等邊三角形的性質可證△AEG≌△FED，可得DF=AG，根據三角形的三邊關系，可得當點A，點G，點D三點共線時，AG值最小，即DF值最小，則可求線段DF的最小值．

如圖，以ED為邊作等邊△DEG，連接AD，EF，AG，

∵△ABC是等邊三角形，點D是BC中點，

∴BD=CD=5，AD⊥BC

∴AD==5，

∵將線段AE繞點A逆時針旋轉60°得AF，

∴AE=AF，∠EAF=60°，

∴△AEF是等邊三角形，

∴AE=EF，∠AEF=60°，

∵△DEG是等邊三角形

∴DE=EG=3，∠GED=60°=∠AEF

∴∠AEG=∠FED，且AE=EF，EG=DE，

∴△AEG≌△FED（SAS）

∴DF=AG，

∵在△ADG中，AG≥AD-DG

∴當點A，點G，點D三點共線時，AG值最小，即DF值最小，

∴DF最小值=AD-DG=5-3