
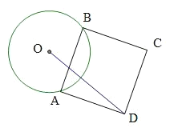
【題目】如圖,⊙O 的半徑為 3,AB 為圓上一動(dòng)弦,以 AB 為邊作正方形 ABCD,求 OD 的最大值__.
【答案】3![]() +3
+3
【解析】
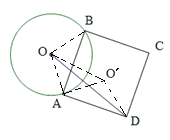
把AO繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90![]() 得到AO′,得到△AOO′是等腰直角三角形,根據(jù)等腰直角三角形的性質(zhì)求出OO′,再根據(jù)正方形的性質(zhì)可得AB=AD,再求出∠BAO=∠DAO′,然后利用“邊角邊”證明△ABO和△ADO′全等,根據(jù)全等三角形對(duì)應(yīng)邊相等可得DO′=BO,再根據(jù)三角形的任意兩邊之和大于第三邊求解即可.
得到AO′,得到△AOO′是等腰直角三角形,根據(jù)等腰直角三角形的性質(zhì)求出OO′,再根據(jù)正方形的性質(zhì)可得AB=AD,再求出∠BAO=∠DAO′,然后利用“邊角邊”證明△ABO和△ADO′全等,根據(jù)全等三角形對(duì)應(yīng)邊相等可得DO′=BO,再根據(jù)三角形的任意兩邊之和大于第三邊求解即可.
如圖,連接AO、BO、把AO繞點(diǎn)A順時(shí)針旋轉(zhuǎn)90![]() 得到AO′,連接DO’
得到AO′,連接DO’
∴△AOO′是等腰直角三角形,
∵AO=3,
∴OO′=![]() =3
=3![]() ,
,
在正方形ABCD中,AB=AD,∠BAD=90![]() ,
,
∵∠BAO+∠BAO′=∠DAO′+∠BAO′=90![]() ,
,
∴∠BAO=∠DAO′,
在△ABO和△ADO′,
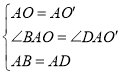 ,
,
∴△ABO≌△ADO′(SAS),
∴DO′=BO=3,
∴OO′+O′D≥OD,
當(dāng)O、O′、D三點(diǎn)共線時(shí),取“=”,
此時(shí),OD的最大值為3![]() +3.
+3.
故答案為:3![]() +3.
+3.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在一個(gè)不透明的盒子中裝有三張卡片,三張卡片的正面分別標(biāo)有數(shù)字![]() ,
,![]() ,
,![]() ,這些卡片除數(shù)字外都相同,將卡片攪勻.
,這些卡片除數(shù)字外都相同,將卡片攪勻.
(1)從盒子中任意抽取一張卡片,恰好抽到標(biāo)有奇數(shù)卡片的概率是_________.
(2)先從盒子中任意抽取一張卡片,再?gòu)挠嘞碌膬蓮埧ㄆ腥我獬槿∫粡埧ㄆ蟪槿〉膬蓮埧ㄆ瑯?biāo)有數(shù)字之和大于![]() 的概率(請(qǐng)用畫樹狀圖或列表等方法求解).
的概率(請(qǐng)用畫樹狀圖或列表等方法求解).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)計(jì)算:(﹣3)2﹣(π﹣4)0+(![]() )﹣2;
)﹣2;
(2)(a+2)2+(1﹣a)(1+a).
(3)解方程:![]() =
=![]() ;
;
(4)解不等式組: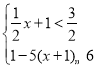
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在ABCD中,以點(diǎn)A為圓心AB長(zhǎng)為半徑畫弧交AD于點(diǎn)F,再分別以點(diǎn)B,F為圓心,大于![]() BF的長(zhǎng)度為半徑畫弧,兩弧交于點(diǎn)P;連接AP并延長(zhǎng)交BC于點(diǎn)E,連接EF.
BF的長(zhǎng)度為半徑畫弧,兩弧交于點(diǎn)P;連接AP并延長(zhǎng)交BC于點(diǎn)E,連接EF.
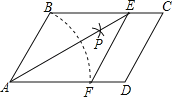
(1)求證:四邊形ABEF是菱形;
(2)若∠C=60°,AE=4![]() ,求菱形ABEF的面積.
,求菱形ABEF的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為配合我市“創(chuàng)建全國(guó)文明城市”某單位計(jì)劃在一塊矩形空地上修建綠色植物園(如圖所示),其中邊靠墻(墻長(zhǎng)為![]() 米),另外三邊用總長(zhǎng)36米的材料圍成.若
米),另外三邊用總長(zhǎng)36米的材料圍成.若![]() 米,矩形
米,矩形![]() 的面積為
的面積為![]() 平方米.
平方米.
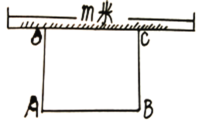
(1)求![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)若矩形面積為160平方米,求![]() 的長(zhǎng).
的長(zhǎng).
(3)在(2)的前提下,墻長(zhǎng)![]() 米對(duì)
米對(duì)![]() 的長(zhǎng)有影響嗎?請(qǐng)?jiān)敿?xì)說明.
的長(zhǎng)有影響嗎?請(qǐng)?jiān)敿?xì)說明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)),與
的左側(cè)),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為拋物線頂點(diǎn);
為拋物線頂點(diǎn);
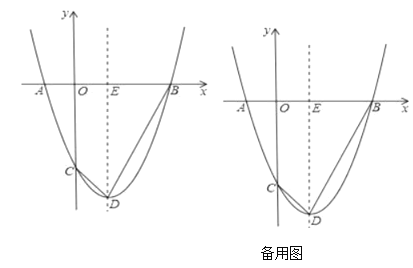
(1)求點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)連結(jié)![]() 、
、![]() ,拋物線的對(duì)稱軸與
,拋物線的對(duì)稱軸與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
①若線段![]() 上有一點(diǎn)
上有一點(diǎn)![]() ,使
,使![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②若拋物線上一點(diǎn)![]() ,作
,作![]() ,交直線
,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,使
,使![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
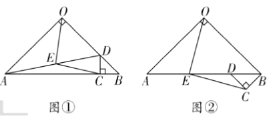
【題目】如圖①,在![]() 中,
中,![]() 為
為![]() 邊上一點(diǎn),過
邊上一點(diǎn),過![]() 點(diǎn)作
點(diǎn)作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,
,![]() 為
為![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() .
.
(觀察猜想)
(1)①![]() 的數(shù)量關(guān)系是___________
的數(shù)量關(guān)系是___________
②![]() 的數(shù)量關(guān)系是______________
的數(shù)量關(guān)系是______________
(類比探究)
(2)將圖①中![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)
逆時(shí)針旋轉(zhuǎn)![]() ,如圖②所示,則(1)中的結(jié)論是否仍然成立?若成立,請(qǐng)給出證明;若不成立,請(qǐng)說明理由;
,如圖②所示,則(1)中的結(jié)論是否仍然成立?若成立,請(qǐng)給出證明;若不成立,請(qǐng)說明理由;
(拓展遷移)
(3)將![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn)任意角度,若
旋轉(zhuǎn)任意角度,若![]() ,請(qǐng)直接寫出點(diǎn)
,請(qǐng)直接寫出點(diǎn)![]() 在同一直線上時(shí)
在同一直線上時(shí)![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明經(jīng)過市場(chǎng)調(diào)查,整理出他媽媽商店里一種商品在第![]() 天的銷售量的相關(guān)信息如下表:
天的銷售量的相關(guān)信息如下表:
時(shí)間第 |
|
|
售價(jià)(元/件) |
| 50 |
每天銷量(件) |
| |
已知該商品的進(jìn)價(jià)為每件20元,設(shè)銷售該商品的每天利潤(rùn)為![]() 元.
元.
(1)求出![]() 與
與![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)問銷售該商品第幾天時(shí),當(dāng)天銷售利潤(rùn)最大,最大利潤(rùn)是多少?
(3)該商品在銷售過程中,共有多少天每天銷售利潤(rùn)不低于2400元?請(qǐng)直接寫出結(jié)果.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD的邊長(zhǎng)是3,BP=CQ,連接AQ,DP交于點(diǎn)O,并分別與邊CD,BC交于點(diǎn)F,E,連接AE,下列結(jié)論:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四邊形OECF;④當(dāng)BP=1時(shí),tan∠OAE=![]() ,其中正確結(jié)論的個(gè)數(shù)是( )
,其中正確結(jié)論的個(gè)數(shù)是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com