
【題目】如圖,拋物線y=-x2+2x+m+1(m為常數(shù))交y軸于點A,與x軸的一個交點在2和3之間,頂點為B.
①拋物線y=-x2+2x+m+1與直線y=m+2有且只有一個交點;
②若點M(-2,y1)、點N(![]() ,y2)、點P(2,y3)在該函數(shù)圖象上,則y1<y2<y3;
,y2)、點P(2,y3)在該函數(shù)圖象上,則y1<y2<y3;
③將該拋物線向左平移2個單位,再向下平移2個單位,所得拋物線解析式為y=-(x+1)2+m;
④點A關(guān)于直線x=1的對稱點為C,點D、E分別在x軸和y軸上,當(dāng)m=1時,四邊形BCDE周長的最小值為![]() .
.
其中正確判斷有( )
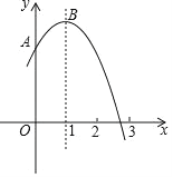
A.①②③④B.②③④C.①③④D.①③
【答案】C
【解析】
將二次函數(shù)配方成![]() 即可判斷①③;將P根據(jù)對稱性轉(zhuǎn)化到對稱軸左邊即可判斷②;將m=1代入函數(shù)解析式即可求算A,C坐標(biāo),作對稱根據(jù)兩點之間線段最短即可求算四邊形BCDE周長的最小值.
即可判斷①③;將P根據(jù)對稱性轉(zhuǎn)化到對稱軸左邊即可判斷②;將m=1代入函數(shù)解析式即可求算A,C坐標(biāo),作對稱根據(jù)兩點之間線段最短即可求算四邊形BCDE周長的最小值.
解:將y=-x2+2x+m+1化為頂點式為:![]()
∴頂點坐標(biāo)為![]() ,函數(shù)圖形與直線y=m+2相切,只有一個公共點,①正確;
,函數(shù)圖形與直線y=m+2相切,只有一個公共點,①正確;
根據(jù)“上加下減,左加右減”將![]() 向左平移2個單位,再向下平移2個單位得到:
向左平移2個單位,再向下平移2個單位得到: ![]() ,③正確;
,③正確;
二次函數(shù)的對稱軸是直線![]() ,故P(2,y3)可對稱到
,故P(2,y3)可對稱到![]() ,在對稱軸左側(cè),y隨x的增大而增大,故
,在對稱軸左側(cè),y隨x的增大而增大,故![]() ,②錯誤;
,②錯誤;
當(dāng)m=1時,函數(shù)解析式為:![]() ,故
,故![]() ,
,![]() ,
,![]()
作B關(guān)于y軸對稱點N,作C關(guān)于x軸對稱點M,則![]() 連接MN,則MN為BE,DE,CD和的最小值,四邊形BCDE周長最小值為MN與BC的和,則有:
連接MN,則MN為BE,DE,CD和的最小值,四邊形BCDE周長最小值為MN與BC的和,則有:
![]()
∴當(dāng)m=1時,四邊形BCDE周長的最小值為![]() ,④正確;
,④正確;
故答案選:C.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在平面直角坐標(biāo)系內(nèi),A,B為x軸上兩點,以AB為直徑的⊙M交y軸于C,D兩點,C為![]() 的中點,弦AE交y軸于點F,且點A的坐標(biāo)為(2,0),CD=8
的中點,弦AE交y軸于點F,且點A的坐標(biāo)為(2,0),CD=8
(1)求⊙M的半徑;
(2)動點P在⊙M的圓周上運動.
①如圖1,當(dāng)FP的長度最大時,點P記為P,在圖1中畫出點P0,并求出點P0橫坐標(biāo)a的值;
②如圖1,當(dāng)EP平分∠AEB時,求EP的長度;
③如圖2,過點D作⊙M的切線交x軸于點Q,當(dāng)點P與點A,B不重合時,請證明![]() 為定值.
為定值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,⊙O經(jīng)過點A、C、D,與BC相交于點E,連接AC、AE.若∠D=70°,則∠EAC的度數(shù)為____________.
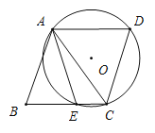
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,兩條高AD,BE交于點P.過點E作
,兩條高AD,BE交于點P.過點E作![]() ,垂足為G,交AD于點F,過點F作
,垂足為G,交AD于點F,過點F作![]() ,交BC于點H,交BE交于點Q,連接DE.
,交BC于點H,交BE交于點Q,連接DE.
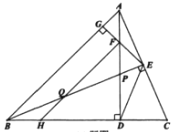
(1)若![]() ,
,![]() ,求DE的長
,求DE的長
(2)若![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖是由邊長為1的小正方形構(gòu)成的網(wǎng)格,每個小正方形的頂點叫做格點.![]() 的頂點在格點上,僅用無刻度尺的直尺在給定網(wǎng)格中畫圖,畫圖過程用虛線表示,畫圖結(jié)果用實線表示,按步驟完成下列問題:
的頂點在格點上,僅用無刻度尺的直尺在給定網(wǎng)格中畫圖,畫圖過程用虛線表示,畫圖結(jié)果用實線表示,按步驟完成下列問題:
(1)將邊![]() 繞點
繞點![]() 順時針旋轉(zhuǎn)90°得到線段
順時針旋轉(zhuǎn)90°得到線段![]() ;
;
(2)畫邊![]() 的中點
的中點![]() ;
;
(3)連接![]() 并延長交
并延長交![]() 于點
于點![]() ,直接寫出
,直接寫出![]() 的值;
的值;
(4)在![]() 上畫點
上畫點![]() ,連接
,連接![]() ,使
,使![]() .
.
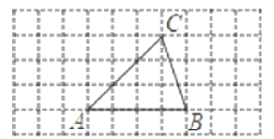
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB=16cm,AC=12cm,動點P、Q分別以每秒2cm和1cm的速度同時開始運動,其中點P從點A出發(fā),沿AC邊一直移到點C為止,點Q從點B出發(fā)沿BA邊一直移到點A為止,(點P到達(dá)點C后,點Q繼續(xù)運動)
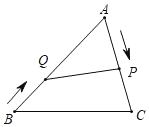
(1)請直接用含t的代數(shù)式表示AP的長和AQ的長,并寫出定義域.
(2)當(dāng)t等于何值時,△APQ與△ABC相似?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】疫情過后,為了促進消費,某商場設(shè)計了一種促銷活動:在一個不透明的箱子里放有四個相同的小球,球上分別標(biāo)有“10元”、“20元”、“30元”和“40元”的字樣,規(guī)定:在本商場同一日內(nèi),顧客每消費滿500元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回)。商場根據(jù)兩小球所標(biāo)金額的和返還相等價格的購物券,購物券可以在本商場消費.某顧客剛好消費500元.
(1)該順客最多可得到______元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于60元的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
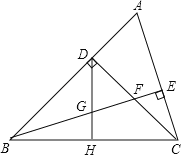
【題目】如圖,△ABC中,∠ABC=45°,CD⊥AB于點D,BE平分∠ABC,且BE⊥AC于點E,與CD交于F,H是BC邊的中點,連接DH與BE交于點G,則下列結(jié)論:
①BF=AC;②∠A=∠DGE;③CE<BG;④S△ADC=S四邊形CEGH;⑤DGAE=DCEF中,正確結(jié)論的個數(shù)是( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=![]() (x>0)的圖象與一次函數(shù)y=ax﹣2(a≠0)的圖象交于點A(3,n).
(x>0)的圖象與一次函數(shù)y=ax﹣2(a≠0)的圖象交于點A(3,n).
(1)求實數(shù)a的值;
(2)設(shè)一次函數(shù)y=ax﹣2(a≠0)的圖象與y軸交于點B,若點C在y軸上,且S△ABC=2S△AOB,求點C的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com