
【題目】如圖,某數學活動小組為測量學校旗桿AB的高度,沿旗桿正前方![]() 米處的點C出發,沿坡角為30°的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈
米處的點C出發,沿坡角為30°的斜坡CD前進4米到達點D,在點D處安置測角儀,測得旗桿頂部A的仰角為37°,量得儀器的高DE為1.5米.已知A、B、C、D、E在同一平面內,AB⊥BC,AB∥DE.求旗桿AB的高度.(參考數據:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() ,計算結果保留根號)
,計算結果保留根號)

科目:初中數學 來源: 題型:
【題目】某校舉行了“防溺水”知識競賽,八年級兩個班選派10名同學參加預賽,依據各參賽選手的成績(均為整數)繪制了統計表和折線統計圖(如圖所示).
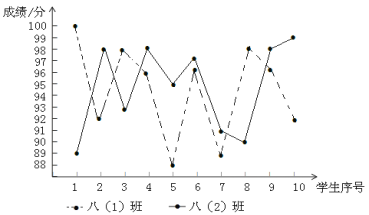
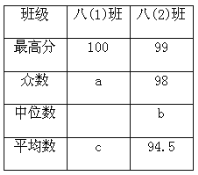
(1)統計表中,a=________, b =________;
(2)若從兩個班的預賽選手中選四名學生參加決賽,其中兩個班的第一名直接進入決賽,另外兩個名額 在成績為98分的學生中任選兩個,求另外兩個決賽名額落在不同班級的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市市民“綠色出行”方式的情況,某校數學興趣小組以問卷調查的形式,隨機調查了某市部分出行市民的主要出行方式(參與問卷調查的市民都只從以下五個種類中選擇一類),并將調查結果繪制成如下不完整的統計圖.
種類 | A | B | C | D | E |
出行方式 | 共享單車 | 步行 | 公交車 | 的士 | 私家車 |
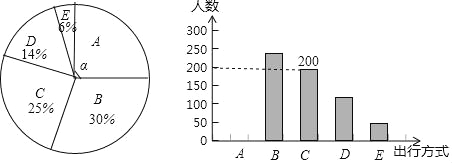
根據以上信息,回答下列問題:
(1)參與本次問卷調查的市民共有 人,其中選擇B類的人數有 人;
(2)在扇形統計圖中,求A類對應扇形圓心角α的度數,并補全條形統計圖;
(3)該市約有12萬人出行,若將A,B,C這三類出行方式均視為“綠色出行”方式,請估計該市“綠色出行”方式的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于二次函數![]() ,有下列結論:①其圖象與x軸一定相交;②若
,有下列結論:①其圖象與x軸一定相交;②若![]() ,函數在
,函數在![]() 時,y隨x的增大而減小;③無論a取何值,拋物線的頂點始終在同一條直線上;④無論a取何值,函數圖象都經過同一個點.其中所有正確的結論是___.(填寫正確結論的序號)
時,y隨x的增大而減小;③無論a取何值,拋物線的頂點始終在同一條直線上;④無論a取何值,函數圖象都經過同一個點.其中所有正確的結論是___.(填寫正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們把1,1,2,3,5,8,13,21,…,這組數稱為斐波那契數列,為了進一步研究,依次以這列數為半徑作90°圓弧 ![]() ,
,![]() ,
,![]() ,…,得到斐波那契螺旋線,然后順次連結P1P2,P2P3,P3P4,…,得到螺旋折線(如圖),已知點P1(0,1),P2(-1,0),P3(0,-1),則該折線上的點P9的坐標為( )
,…,得到斐波那契螺旋線,然后順次連結P1P2,P2P3,P3P4,…,得到螺旋折線(如圖),已知點P1(0,1),P2(-1,0),P3(0,-1),則該折線上的點P9的坐標為( )
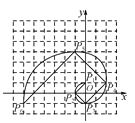
A. (-6,24)B. (-6,25)C. (-5,24)D. (-5,25)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,AB=4,將△ABC繞點A逆時針旋轉60°,得到△ADE,連接CE,則CE等于( )
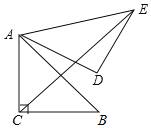
A. 5B. 6C. 2+2![]() D. 2+2
D. 2+2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線y=![]() x2+
x2+![]() x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線l經過A,C兩點,連接BC.
x-2與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,直線l經過A,C兩點,連接BC.
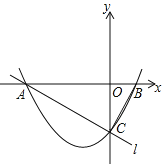
(1)求直線l的解析式;
(2)若直線x=m(m<0)與該拋物線在第三象限內交于點E,與直線l交于點D,連接OD.當OD⊥AC時,求線段DE的長;
(3)取點G(0,-1),連接AG,在第一象限內的拋物線上,是否存在點P,使∠BAP=∠BCO-∠BAG?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
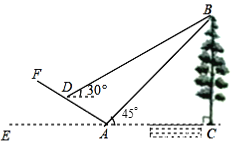
【題目】如圖,小明為了測量小河對岸大樹BC的高度,他在點A測得大樹頂端B的仰角是45°,沿斜坡走![]() 米到達斜坡上點D,在此處測得樹頂端點B的仰角為30°,且斜坡AF的坡比為1︰2.則小明從點A走到點D的過程中,他上升的高度為____米;大樹BC的高度為____米(結果保留根號).
米到達斜坡上點D,在此處測得樹頂端點B的仰角為30°,且斜坡AF的坡比為1︰2.則小明從點A走到點D的過程中,他上升的高度為____米;大樹BC的高度為____米(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
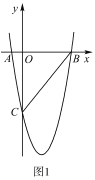
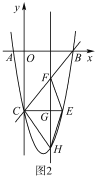
【題目】如圖![]() ,在平面直角角坐標系中,已知拋物線
,在平面直角角坐標系中,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點.
兩點.
(1)求拋物線的函數表達式;
(2)如圖![]() ,
,![]() 軸與拋物線相交于點
軸與拋物線相交于點![]() ,點
,點![]() 是直線
是直線![]() 下方拋物線上的動點,過點
下方拋物線上的動點,過點![]() 且與
且與![]() 軸平行的直線與
軸平行的直線與![]() ,
,![]() 分別交于點
分別交于點![]() 試探究當點
試探究當點![]() 運動到何處時,線段
運動到何處時,線段![]() 的最長,求點
的最長,求點![]() 的坐標;
的坐標;
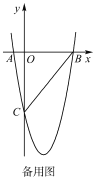
(3)若點![]() 為拋物線的頂點,點
為拋物線的頂點,點![]() 是該拋物線上的一點,在
是該拋物線上的一點,在![]() 軸、
軸、![]() 軸上分別找點
軸上分別找點![]() ,使四邊形
,使四邊形![]() 的周長最小,請求出點
的周長最小,請求出點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com