
【題目】在![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊是一點,連
邊是一點,連![]() ,過點
,過點![]() 作
作![]() 的垂線與過點
的垂線與過點![]() 作
作![]() 的垂線交于點
的垂線交于點![]() 當
當![]() ,
,![]() ,則
,則![]() 的值是_____.
的值是_____.
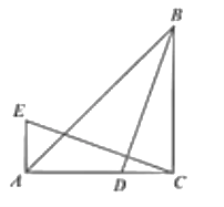
【答案】![]()
【解析】
作DH∥AB交EC于H,設DF=![]() ,證得∠E=∠FDC,∠FDH=∠ABD,在Rt△FDC和Rt△BDC中,利用
,證得∠E=∠FDC,∠FDH=∠ABD,在Rt△FDC和Rt△BDC中,利用![]() ,求得
,求得![]() 、
、![]() 、
、![]() 的長,在Rt△BGF、Rt△FDH中,求得
的長,在Rt△BGF、Rt△FDH中,求得![]() 、
、![]() ,繼而求得
,繼而求得![]() 、
、![]() 的長,利用平行線分線段成比例定理即可求解.
的長,利用平行線分線段成比例定理即可求解.
如圖,作DH∥AB交EC于H,設DF=![]() ,
,
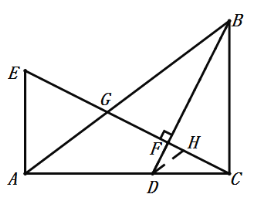
∵AE⊥AC,BC⊥AC,DB⊥EC,
∴∠E+∠ECA=90![]() ,∠FDC+∠ECA =90
,∠FDC+∠ECA =90![]() ,DH∥AB,
,DH∥AB,
∴∠E=∠FDC,∠FDH=∠ABD,
∵![]() ,
,
在Rt△FDC中,∠DFC =90![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△BDC中,∠BCD =90![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△BGF中,∠BFG =90![]() ,
,
![]() ,
,
∴![]() ,
,
在Rt△FDH中,∠DFH =90![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∵DH∥AG,
∴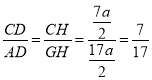 ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C = 90°, P是CB邊上一動點,連接AP,作PQ⊥AP交AB于Q . 已知AC = 3cm,BC = 6cm,設PC的長度為xcm,BQ的長度為ycm .

小青同學根據學習函數的經驗對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小青同學的探究過程,請補充完整:
(1) 按照下表中自變量x的值進行取點、畫圖、測量,分別得到了y的幾組對應值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(說明:補全表格時,相關數據保留一位小數)
m的值約為多少cm;
(2)在平面直角坐標系中,描出以補全后的表格中各組數值所對應的點(x ,y),畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:
①當y > 2時,寫出對應的x的取值范圍;
②若點P不與B,C兩點重合,是否存在點P,使得BQ=BP?(直接寫結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校舉行圖書節義賣活動,將所售款項捐給其他貧困學生.在這次義賣活動中,某班級售書情況如下圖:
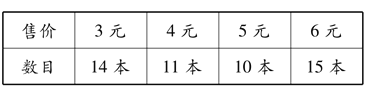
下列說法正確的是( )
A.該班級所售圖書的總數收入是226元
B.在該班級所售圖書價格組成的一組數據中,中位數是4
C.在該班級所售圖書價格組成的一組數據中,眾數是15
D.在該班級所售圖書價格組成的一組數據中,方差是2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車同時從A地出發,勻速開往B地,甲車行駛到B地后立即沿原路線以原速度返回A地,到達A地后停止運動:當甲車到達A地時,乙車恰好到達B地,并停止運動.已知甲車的速度為150km/h,設甲車出發xh后,甲、乙兩車之間的距離為ykm,圖中的折線OMNQ表示了整個運動過程中y與x之間的函數關系.

(1)A、B兩地的距離是 km,乙車的速度是 km/h;
(2)指出點M的實際意義,并求線段MN所表示的y與x之間的函數表達式;
(3)當兩車相距50km時,直接寫出x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
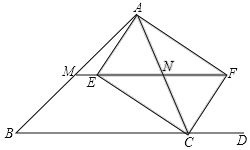
【題目】如圖:在△ABC中,CE、CF分別平分∠ACB與它的鄰補角∠ACD,AE⊥CE于E,AF⊥CF于F,直線EF分別交AB、AC于M、N.
(1)求證:四邊形AECF為矩形;
(2)試猜想MN與BC的關系,并證明你的猜想;
(3)如果四邊形AECF是菱形,試判斷△ABC的形狀,直接寫出結果,不用說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 中,
中,![]() 過
過![]() 其中一個頂點的直線把
其中一個頂點的直線把![]() 分成兩個等腰三角形.
分成兩個等腰三角形.
(1)如圖1,若![]() 求
求![]() 的值;
的值;

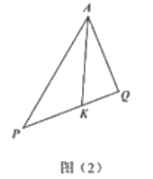
(2)![]() 度(
度(![]() 除外) ;
除外) ;
(3)如圖2,![]() 為銳角,
為銳角,![]() 在
在![]() 延長線上,
延長線上,![]() 在邊
在邊![]() 上,
上,![]() 平分
平分![]() 交
交![]() 于
于![]() 請求線段
請求線段![]()
![]() 三者之者的數量關系. (用
三者之者的數量關系. (用![]() 表示)
表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
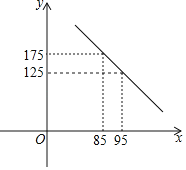
【題目】武漢“新冠肺炎”發生以來,某醫療公司積極復工,加班加點生產醫用防護服,為防控一線助力.以下是該公司以往的市場調查,發現該公司防護服的日銷售量y(套)與銷售單價x(元)之間滿足一次函數關系,如下圖所示,關于日銷售利潤w(元)和銷售單價x(元)的幾組對應值如下表:
銷售單價x(元) | 85 | 95 | 105 |
日銷售利潤w(元) | 875 | 1875 | 1875 |
(注:日銷售利潤=日銷售量×(銷售單價一成本單價))
(1)求y關于x的函數解析式(不要求寫出x的取值范圍);
(2)根據函數圖象和表格所提供的信息,填空:
該公司生產的防護服的成本單價是 元,當銷售單價x= 元時,日銷售利潤w最大,最大值是 元;
(3)該公司復工以后,在政府部門的幫助下,原材料采購成本比以往有了下降,平均起來,每生產一套防護服,成本比以前下降5元.該公司計劃開展科技創新,以降低該產品的成本,如果在今后的銷售中,日銷售量與銷售單價仍存在(1)中的關系.若想實現銷售單價為90元時,日銷售利潤不低于3750元的銷售目標,該產品的成本單價應不超過多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
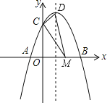
【題目】如圖,對稱軸為![]() 的拋物線
的拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,其中
點,其中![]() 點坐標為
點坐標為![]() 設拋物線的頂點為
設拋物線的頂點為![]() .
.
![]() 求拋物線的解析式及頂點坐標;
求拋物線的解析式及頂點坐標;
![]() 為
為![]() 軸上的一點,當
軸上的一點,當![]() 的周長最小時,求點
的周長最小時,求點![]() 的坐標及
的坐標及![]() 的周長.
的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com