
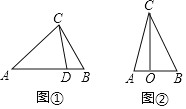
【題目】如圖①在![]() 中,若點
中,若點![]() 在邊
在邊![]() 上,且
上,且![]() 則點
則點![]() 定義為
定義為![]() 的邊
的邊![]() 上的“金點”.
上的“金點”.
![]() 已知點
已知點![]() 是
是![]() 的邊
的邊![]() 上的“金點”:
上的“金點”:
①若![]() 則
則![]() 的長為 _;
的長為 _;
②若![]() 則
則![]() 的長為 _;
的長為 _;
![]() 在圖①中,若點
在圖①中,若點![]() 是
是![]() 的邊
的邊![]() 的中點,
的中點,![]() 試判斷點
試判斷點![]() 是不是
是不是![]() 的“金
的“金
點”,并說明理由;
![]() 如圖②,已知點
如圖②,已知點![]() 為同一直線上三點,且
為同一直線上三點,且![]() 在
在![]() 所在直線上是否存在一點
所在直線上是否存在一點![]() 使點
使點![]() 中的某一點是其余三點圍成的三角形的“金點”.若存在,求出線段
中的某一點是其余三點圍成的三角形的“金點”.若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(1)①![]() 或
或![]() ; ②
; ②![]() ;(2)點
;(2)點![]() 是
是![]() 的“金點”,理由見解析;(3)存在,滿足條件的
的“金點”,理由見解析;(3)存在,滿足條件的![]() 長為
長為![]() 或
或![]() .
.
【解析】
(1)①分兩種情形,利用相似三角形的性質(zhì)解決問題即可.②利用相似三角形的性質(zhì)解決問題即可.
(2)結(jié)論:點D是△ABC的“金點”.只要證明△ACD∽△ABC即可解決問題;
(3)如圖③中,存在.有三種情形:過點A作MA⊥AC交CB的延長線于M,作MH⊥y軸于H.構(gòu)造全等三角形,利用平行線分線段成比例定理構(gòu)建方程求出點C坐標,分三種情形求解即可解決問題;
(1)![]() 若
若![]() 如圖:
如圖:

∵![]()
∴![]() .
.
∴![]()
∴![]()
∴![]()
若![]() 如圖:
如圖:
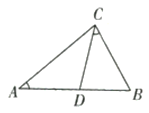
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
![]() 如圖所示:
如圖所示:
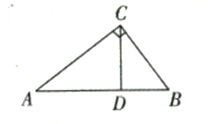
∵點![]() 是
是![]() 的“金點”,
的“金點”,
∴![]() 或
或![]()
當![]() 時,
時,
∵![]()
∴![]()
∴![]() ;
;
當![]() 時,
時,
同理可證![]() .
.
在![]() 中,由勾股定理得,
中,由勾股定理得,
![]()
∵![]()
∴![]()
故答案為:①![]() 或
或![]() ; ②
; ②![]() ;
;
(2)點![]() 是
是![]() 的“金點”,
的“金點”,
理由如下:
∵點![]() 是
是![]() 的邊
的邊![]() 的中點,
的中點,![]()
∴![]()
又∵![]()
∴![]()
![]()
∴![]()
又![]()
![]()
∴![]()
所以點![]() 是
是![]() 的“金點”;
的“金點”;
故答案為:點![]() 是
是![]() 的“金點”,理由見解析.
的“金點”,理由見解析.
(3)存在.
有三種情形:
如圖所示:過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.

∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]() .
.
設(shè)![]()
∵![]()
∴![]()
∵![]()
∵![]() .
.
∴![]()
∴![]()
解得![]() 或
或![]() (舍去),
(舍去),
∴![]()
![]() 當
當![]() 時,點
時,點![]() 是
是![]() 的“金點”設(shè)
的“金點”設(shè)![]()
∵![]() ,
,
∴![]()
∴![]() ,即
,即![]() .
.
∴![]() ,
,
解得![]()
∴![]() .
.
![]() 當
當![]() 時,點
時,點![]() 是
是![]() 的“金點”
的“金點”
易知![]() ,
,
∴![]() .
.
![]() 當
當![]() 時,點
時,點![]() 是
是![]() 的“金點”
的“金點”
易知![]() ,
,
∴![]() .
.
綜上所述,滿足條件的![]() 長為
長為![]() 或
或![]() .
.
故答案為:存在,OD長為42或6


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數(shù)學 來源: 題型:
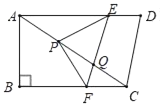
【題目】如圖,四邊形ABCD中,∠B=90°,AD∥BC,AD=AC,AB=6,BC=8.點P以每秒5個單位長度由點A沿線段AC運動;同時,線段EF以相同的速度由CD出發(fā)沿DA方向平移,與AC交于點Q,連結(jié)PE,PF.當點F與點B重合時,停止所有運動,設(shè)P運動時間為t秒.
(1)求證:△APE≌△CFP.
(2)當t<1時,若△PEF為直角三角形,求t的值.
(3)作△PEF的外接圓⊙O.
①當⊙O只經(jīng)過線段AC的一個端點時,求t的值.
②作點P關(guān)于EF的對稱點P′,當P′落在CD上時,請直接寫出線段CP′的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,直線y1=﹣![]() x與雙曲線y=
x與雙曲線y=![]() 交于A,B兩點,點C在x軸上,連接AC,BC.當AC⊥BC,S△ABC=15時,求k的值為( )
交于A,B兩點,點C在x軸上,連接AC,BC.當AC⊥BC,S△ABC=15時,求k的值為( )

A.﹣10B.﹣9C.6D.4
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為加強公民節(jié)電意識,某縣將居民用電量分為兩個階梯,月用電量不超過![]() 度時按第一個階梯費用收費,超過
度時按第一個階梯費用收費,超過![]() 度時,超出的部分按第二個階梯費用收費下表是該縣居民肖偉家2019年3月和4月所交電費的收據(jù).求該縣居民用電第--階梯電費和第二階梯電費分別為每度多少元?
度時,超出的部分按第二個階梯費用收費下表是該縣居民肖偉家2019年3月和4月所交電費的收據(jù).求該縣居民用電第--階梯電費和第二階梯電費分別為每度多少元?
電費收據(jù)(幸福里小區(qū)電費專用章)
戶名 | 肖偉 |
電表號 |
|
月份 | 3月 |
用電量 |
|
金額 |
|
2019年3月收費員林云
電費收據(jù)(幸福里小區(qū)電費專用章)
戶名 | 肖偉 |
電表號 |
|
月份 | 4月 |
用電量 |
|
金額 |
|
2019年4月收費員林云
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在圓O中,弦AB與CD相交于點E,且弧AC與弧BD相等.點D在劣弧AB上,聯(lián)結(jié)CO并延長交線段AB于點F,聯(lián)結(jié)OA、OB.當OA=![]() ,且tan∠OAB=
,且tan∠OAB=![]() .
.
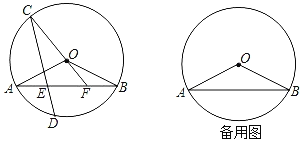
(1)求弦CD的長;
(2)如果△AOF是直角三角形,求線段EF的長;
(3)如果S△CEF=4S△BOF,求線段AF的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】學校實施新課程改革以來,學生的學習能力有了很大提高.王老師為進一步了解本班學生自主學習、合作交流的現(xiàn)狀,對該班部分學生進行調(diào)查,把調(diào)查結(jié)果分成四類(A:特別好,B:好,C:一般,D:較差)后,再將調(diào)查結(jié)果繪制成兩幅不完整的統(tǒng)計圖(如圖1,2).請根據(jù)統(tǒng)計圖解答下列問題:

(1)本次調(diào)查中,王老師一共調(diào)查了 名學生;
(2)將條形統(tǒng)計圖補充完整;
(3)為了共同進步,王老師從被調(diào)查的A類和D類學生中分別選取一名學生進行“兵教兵”互助學習,請用列表或畫樹狀圖的方法求出恰好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,點A(-2,m)繞坐標原點O順時針旋轉(zhuǎn)90°后,恰好落在圖中⊙P中的陰影區(qū)域(包括邊界)內(nèi),⊙P的半徑為1,點P的坐標為(3,2),則m的取值范圍是______.
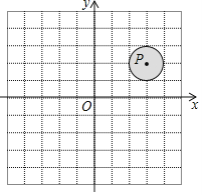
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖是一款拋物線型落地燈筒示意圖,防滑螺母C為拋物線支架的最高點,燈罩D距離地面1.5米,最高點C距燈柱的水平距離為1.6米,燈柱AB1.5米,若茶幾擺放在燈罩的正下方,則茶幾到燈柱的距離AE為多少米( )
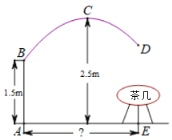
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com