
【題目】如圖1,平行四邊形![]() 在平面直角坐標(biāo)系中,
在平面直角坐標(biāo)系中,![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè))兩點(diǎn)的橫坐標(biāo)是方程
的左側(cè))兩點(diǎn)的橫坐標(biāo)是方程![]() 的兩個(gè)根,點(diǎn)
的兩個(gè)根,點(diǎn)![]() 在
在![]() 軸上,其中
軸上,其中![]() .
.
![]() 若
若![]() 是第一象限位于直線
是第一象限位于直線![]() 上方的一點(diǎn),過(guò)
上方的一點(diǎn),過(guò)![]() 作
作![]() 于
于![]() 過(guò)
過(guò)![]() 作
作![]() 軸于
軸于![]() 點(diǎn),作
點(diǎn),作![]() 軸交直線
軸交直線![]() 于
于![]() 為
為![]() 中點(diǎn),其中
中點(diǎn),其中![]() 的周長(zhǎng)是
的周長(zhǎng)是![]() ;若
;若![]() 為線段
為線段![]() 上一動(dòng)點(diǎn),
上一動(dòng)點(diǎn),![]() 為直線
為直線![]() 上一動(dòng)點(diǎn),連接
上一動(dòng)點(diǎn),連接![]() ,求
,求![]() 的最小值,此時(shí)
的最小值,此時(shí)![]() 軸上有一個(gè)動(dòng)點(diǎn)
軸上有一個(gè)動(dòng)點(diǎn)![]() ,當(dāng)
,當(dāng)![]() 最大時(shí),求
最大時(shí),求![]() 點(diǎn)坐標(biāo);
點(diǎn)坐標(biāo);
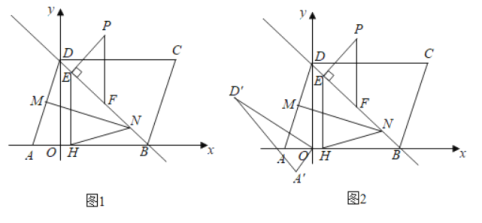
![]() 在
在![]() 的情況下,將
的情況下,將![]() 繞
繞![]() 點(diǎn)逆時(shí)針旋轉(zhuǎn)
點(diǎn)逆時(shí)針旋轉(zhuǎn)![]() 后得到
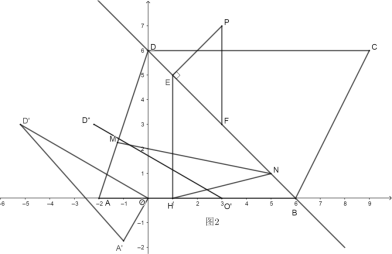
后得到![]() 如圖2,將線段
如圖2,將線段![]() 沿著
沿著![]() 軸平移記平移過(guò)程中的線段
軸平移記平移過(guò)程中的線段![]() 為
為![]() ,在平面直角坐標(biāo)系中是否存在點(diǎn)
,在平面直角坐標(biāo)系中是否存在點(diǎn)![]() ,使得以點(diǎn)
,使得以點(diǎn)![]() 為頂點(diǎn)的四邊形為菱形,若存在,請(qǐng)求出點(diǎn)
為頂點(diǎn)的四邊形為菱形,若存在,請(qǐng)求出點(diǎn)![]() 的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由.
【答案】(1)![]() ;(2)存在,點(diǎn)
;(2)存在,點(diǎn)![]() 的坐標(biāo)為:
的坐標(biāo)為: ![]() ,
,![]() ,
,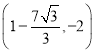
【解析】
(1)通過(guò)解方程![]() ,求得點(diǎn)A、B的坐標(biāo),結(jié)合圖形得到點(diǎn)C、D、E的坐標(biāo),
,求得點(diǎn)A、B的坐標(biāo),結(jié)合圖形得到點(diǎn)C、D、E的坐標(biāo),![]() ,
,![]() 軸,得到
軸,得到![]() 為等腰直角三角形,由周長(zhǎng)可以求出三邊長(zhǎng),利用“將軍飲馬”模型,兩動(dòng)一定求出
為等腰直角三角形,由周長(zhǎng)可以求出三邊長(zhǎng),利用“將軍飲馬”模型,兩動(dòng)一定求出![]() 最小值,以及兩定一動(dòng)求出
最小值,以及兩定一動(dòng)求出![]() 最大值即可;
最大值即可;
(2)根據(jù)題意,設(shè)點(diǎn)![]() ,則
,則![]() ,
,![]() ,表示出E
,表示出E![]() ,E
,E![]() ,若以點(diǎn)
,若以點(diǎn)![]() 為頂點(diǎn)的四邊形為菱形,則分三種情況討論,分別利用鄰邊相等即可求出.
為頂點(diǎn)的四邊形為菱形,則分三種情況討論,分別利用鄰邊相等即可求出.
![]() 由題意可得:
由題意可得:
∵解方程![]() 的兩個(gè)根分別為:
的兩個(gè)根分別為:![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)
的左側(cè)
∴![]() ,
,
直線![]() ,
,
直線![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形,
![]() 的周長(zhǎng)為
的周長(zhǎng)為![]() ,
,
![]() ,
,
![]() ,
,
點(diǎn)![]() 關(guān)于
關(guān)于![]() 的對(duì)稱點(diǎn)為:
的對(duì)稱點(diǎn)為:![]()
過(guò)點(diǎn)![]() 做
做![]() 分別交
分別交![]() 、
、![]() 于點(diǎn)
于點(diǎn)![]() ,
,
則![]() ,
,
此時(shí)![]() 的值最小為
的值最小為![]() ,
,
則![]() ,
,
點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對(duì)稱
軸對(duì)稱![]() ,
,
直線![]()
![]() ,
,
故答案為:![]() .
.
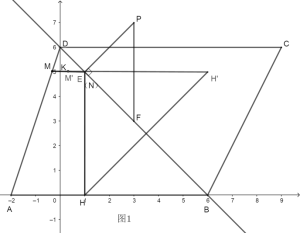
![]() 存在.
存在.
設(shè)點(diǎn)![]() ,則
,則![]() ,
,![]()
由題意可得: ![]() ,
,
![]() ,
,![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
解得:![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為:
的坐標(biāo)為:![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
解得:![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為:
的坐標(biāo)為:![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
解得:![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為:
的坐標(biāo)為: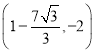 ,
,
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)為:
的坐標(biāo)為: ![]() ,
,![]() ,
,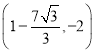 ,
,
故答案為:![]() ,
,![]() ,
,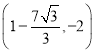 .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】蛋黃酥是現(xiàn)下糕點(diǎn)界的網(wǎng)紅,每一顆蛋黃酥金黃誘人的酥皮下都包著一顆細(xì)膩綿沙的咸蛋黃,其口口酥心,層層松軟的特點(diǎn)讓人難忘.某商家推出兩款八粒裝的蛋黃酥,其中麻薯豆沙蛋黃酥50元每盒,蓮蓉千層蛋黃酥48元每盒,兩款蛋黃酥非常暢銷,平均每周銷售額為344000元.
(1)受生產(chǎn)能力限制,該商家平時(shí)每周生產(chǎn)7000盒八粒裝蛋黃酥,為了保證周銷售額不變,則每周平均需生產(chǎn)麻薯豆沙蛋黃酥多少盒?
(2)在(1)的條件下,為了迎接雙十一大促,該商家提前擴(kuò)大生產(chǎn)能力,并在雙十一當(dāng)天,開展蛋黃酥促銷活動(dòng),麻薯豆沙蛋黃酥售價(jià)降低了![]() a元,其銷量在當(dāng)天比平時(shí)周銷量增加了2000盒,最后當(dāng)天兩款蛋黃酥的總銷售額比平時(shí)周銷售額還多96000元,求a的值.
a元,其銷量在當(dāng)天比平時(shí)周銷量增加了2000盒,最后當(dāng)天兩款蛋黃酥的總銷售額比平時(shí)周銷售額還多96000元,求a的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
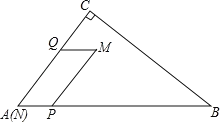
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點(diǎn)
.點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 以每秒1個(gè)單位的速度向終點(diǎn)
以每秒1個(gè)單位的速度向終點(diǎn)![]() 運(yùn)動(dòng);同時(shí),點(diǎn)
運(yùn)動(dòng);同時(shí),點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 以每秒2個(gè)單位的速度向終點(diǎn)
以每秒2個(gè)單位的速度向終點(diǎn)![]() 運(yùn)動(dòng),當(dāng)
運(yùn)動(dòng),當(dāng)![]() 、
、![]() 兩點(diǎn)其中一點(diǎn)到達(dá)點(diǎn)
兩點(diǎn)其中一點(diǎn)到達(dá)點(diǎn)![]() 時(shí),另一點(diǎn)也隨之停止運(yùn)動(dòng),過(guò)點(diǎn)
時(shí),另一點(diǎn)也隨之停止運(yùn)動(dòng),過(guò)點(diǎn)![]() 作
作![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() .當(dāng)點(diǎn)
.當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 不重合時(shí),以
不重合時(shí),以![]() 、
、![]() 為鄰邊作
為鄰邊作![]() .設(shè)
.設(shè)![]() 、
、![]() 兩點(diǎn)的運(yùn)動(dòng)時(shí)間為
兩點(diǎn)的運(yùn)動(dòng)時(shí)間為![]() 秒.
秒.
(1)求線段![]() 的長(zhǎng).(用含
的長(zhǎng).(用含![]() 的代數(shù)式表示)
的代數(shù)式表示)
(2)點(diǎn)![]() 在邊
在邊![]() 上運(yùn)動(dòng),當(dāng)點(diǎn)
上運(yùn)動(dòng),當(dāng)點(diǎn)![]() 落在邊
落在邊![]() 上時(shí),求
上時(shí),求![]() 的值.
的值.
(3)設(shè)![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 在
在![]() 內(nèi)部時(shí),求
內(nèi)部時(shí),求![]() 與
與![]() 之間的函數(shù)關(guān)系式.
之間的函數(shù)關(guān)系式.
(4)當(dāng)![]() 的一邊是它鄰邊2倍時(shí),直接寫出
的一邊是它鄰邊2倍時(shí),直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為直線
為直線![]() 上一動(dòng)點(diǎn)(點(diǎn)
上一動(dòng)點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() 重合),以
重合),以![]() 為腰作等腰直角
為腰作等腰直角![]() ,使
,使![]() ,連接
,連接![]() .
.
(1)觀察猜想
如圖1,當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),
上時(shí),
①![]() 與
與![]() 的位置關(guān)系為__________;
的位置關(guān)系為__________;
②![]() 之間的數(shù)量關(guān)系為___________(提示:可證
之間的數(shù)量關(guān)系為___________(提示:可證![]() )
)

(2)數(shù)學(xué)思考
如圖2,當(dāng)點(diǎn)![]() 在線段
在線段![]() 的延長(zhǎng)線上時(shí),(1)中的①、②結(jié)論是否仍然成立?若成立,請(qǐng)給予證明;若不成立,請(qǐng)你寫出正確結(jié)論再給予證明;
的延長(zhǎng)線上時(shí),(1)中的①、②結(jié)論是否仍然成立?若成立,請(qǐng)給予證明;若不成立,請(qǐng)你寫出正確結(jié)論再給予證明;
(3)拓展延伸
如圖3,當(dāng)點(diǎn)![]() 在線段
在線段![]() 的延長(zhǎng)線時(shí),將
的延長(zhǎng)線時(shí),將![]() 沿線段
沿線段![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合,連接
重合,連接![]() ,若
,若![]() ,請(qǐng)直接寫出線段
,請(qǐng)直接寫出線段![]() 的長(zhǎng).(提示:做
的長(zhǎng).(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】A、B、C三瓶不同濃度的酒精,A瓶?jī)?nèi)有酒精2kg,濃度x%,B瓶有酒精3kg,濃度y%,C瓶有酒精5kg,濃度z%,從A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后測(cè)得濃度33.5%,將混合后的溶液倒回瓶中,使它們恢復(fù)原來(lái)的質(zhì)量,再?gòu)?/span>A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后測(cè)得濃度為31.5%,測(cè)量發(fā)現(xiàn)![]() ,
,![]() ,
,![]() ,且x、y、z均為整數(shù),則把起初A、B兩瓶酒精全部混合后的濃度為______.
,且x、y、z均為整數(shù),則把起初A、B兩瓶酒精全部混合后的濃度為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
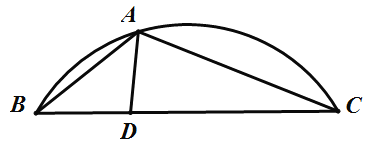
【題目】如圖,A是![]() 上一動(dòng)點(diǎn),D是弦BC上一定點(diǎn),連接AB,AC,AD.設(shè)線段AB的長(zhǎng)是xcm,線段AC的長(zhǎng)是
上一動(dòng)點(diǎn),D是弦BC上一定點(diǎn),連接AB,AC,AD.設(shè)線段AB的長(zhǎng)是xcm,線段AC的長(zhǎng)是![]() cm,線段AD的長(zhǎng)是
cm,線段AD的長(zhǎng)是![]() cm.
cm.
小騰根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗(yàn),分別對(duì)函數(shù)![]() ,
,![]() 隨自變量x的變化的關(guān)系進(jìn)行了探究.下面是小騰的探究過(guò)程,請(qǐng)補(bǔ)充完整:
隨自變量x的變化的關(guān)系進(jìn)行了探究.下面是小騰的探究過(guò)程,請(qǐng)補(bǔ)充完整:
(1)對(duì)于點(diǎn)A在![]() 上的不同位置,畫圖、測(cè)量,得到了
上的不同位置,畫圖、測(cè)量,得到了![]() ,
,![]() 的長(zhǎng)度與x的幾組值:
的長(zhǎng)度與x的幾組值:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
x/cm | 0.00 | 0.99 | 2.01 | 3.46 | 4.98 | 5.84 | 7.07 | 8.00 |
| 8.00 | 7.46 | 6.81 | 5.69 | 4.26 | 3.29 | 1.62 | 0.00 |
| 2.50 | 2.08 | 1.88 | 2.15 | 2.99 | 3.61 | 4.62 | m |
請(qǐng)直接寫出上表中的m值是 ;
(2)在同一平面直角坐標(biāo)系![]() 中,描出補(bǔ)全后表中各組數(shù)據(jù)所對(duì)應(yīng)的點(diǎn)(x,
中,描出補(bǔ)全后表中各組數(shù)據(jù)所對(duì)應(yīng)的點(diǎn)(x,![]() ),(x,
),(x,![]() ),并畫出函數(shù)
),并畫出函數(shù)![]() ,
,![]() 的圖象;
的圖象;
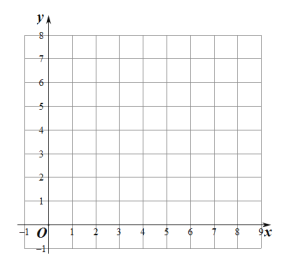
(3)結(jié)合函數(shù)圖象,解決問(wèn)題:當(dāng)AC=AD時(shí),AB的長(zhǎng)度約為 cm;當(dāng)AC=2AD時(shí),AB的長(zhǎng)度約為 cm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一個(gè)不透明的袋子中,裝有除顏色外其余均相同的紅、藍(lán)兩種球,已知其中紅球有3個(gè),且從中任意摸出一個(gè)是紅球的概率為0.75.
(1)根據(jù)題意,袋中有 個(gè)藍(lán)球.
(2)若第一次隨機(jī)摸出一球,不放回,再隨機(jī)摸出第二個(gè)球.請(qǐng)用畫樹狀圖或列表法求“摸到兩球中至少一個(gè)球?yàn)樗{(lán)球(記為事件A)”的概率P(A).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
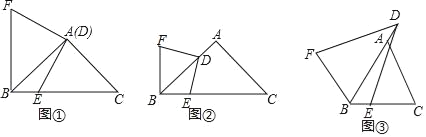
【題目】觀察猜想:(1)如圖①,在Rt△ABC中,∠BAC=90°,AB=AC=3,點(diǎn)D與點(diǎn)A重合,點(diǎn)E在邊BC上,連接DE,將線段DE繞點(diǎn)D順時(shí)針旋轉(zhuǎn)90°得到線段DF,連接BF,BE與BF的位置關(guān)系是 ,BE+BF= ;
探究證明:(2)在(1)中,如果將點(diǎn)D沿AB方向移動(dòng),使AD=1,其余條件不變,如圖②,判斷BE與BF的位置關(guān)系,并求BE+BF的值,請(qǐng)寫出你的理由或計(jì)算過(guò)程;
拓展延伸:(3)如圖③,在△ABC中,AB=AC,∠BAC=a,點(diǎn)D在邊BA的延長(zhǎng)線上,BD=n,連接DE,將線段DE繞著點(diǎn)D順時(shí)針旋轉(zhuǎn),旋轉(zhuǎn)角∠EDF=a,連接BF,則BE+BF的值是多少?請(qǐng)用含有n,a的式子直接寫出結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
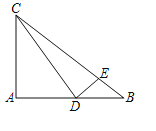
【題目】在Rt△ABC中,∠A=90°,AB=4,AC=3,D為AB邊上一動(dòng)點(diǎn)(點(diǎn)D與點(diǎn)A、B不重合),聯(lián)結(jié)CD,過(guò)點(diǎn)D作DE⊥DC交邊BC于點(diǎn)E.
(1)如圖,當(dāng)ED=EB時(shí),求AD的長(zhǎng);
(2)設(shè)AD=x,BE=y,求y關(guān)于x的函數(shù)解析式并寫出函數(shù)定義域;
(3)把△BCD沿直線CD翻折得△CDB',聯(lián)結(jié)AB',當(dāng)△CAB'是等腰三角形時(shí),直接寫出AD的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com