
【題目】綜合與實踐
問題情境:
如圖1,已知點![]() 是正方形
是正方形![]() 的兩條對角線的交點,以點
的兩條對角線的交點,以點![]() 為直角頂點的直角三角形
為直角頂點的直角三角形![]() 的兩邊
的兩邊![]() ,
,![]() 分別過點
分別過點![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.

(1)![]() 的長度為________;
的長度為________;
操作證明:
(2)如圖2,在(1)的條件下,將![]() 按如圖放置,若
按如圖放置,若![]() ,
,![]() 分別與
分別與![]() ,
,![]() 相交于點
相交于點![]() ,
,![]() .請判斷
.請判斷![]() 和
和![]() 有怎樣的數量關系,并證明結論;
有怎樣的數量關系,并證明結論;

探究發現:
(3)如圖3,在(1)的條件下,將![]() 按如圖放置,若點
按如圖放置,若點![]() 恰好在
恰好在![]() 上,求證:
上,求證:![]() .
.

【答案】(1)![]() ;(2)
;(2)![]() ,證明詳見解析;(3)詳見解析
,證明詳見解析;(3)詳見解析
【解析】
(1)由題意可得OC=OB,OC⊥OB,再根據勾股定理即可得到答案;
(2)連接![]() ,
,![]() ,證明
,證明![]() ,即可得出答案;
,即可得出答案;
(3)根據題意可推出![]() 為等邊三角形,可得
為等邊三角形,可得![]() ,
,![]() ,再根據
,再根據![]() ,可得
,可得![]() ,從而可推出,
,從而可推出,![]() ,即可得證.
,即可得證.
解:(1)∵點![]() 是正方形
是正方形![]() 的兩條對角線的交點,以點
的兩條對角線的交點,以點![]() 為直角頂點的直角三角形
為直角頂點的直角三角形![]() 的兩邊
的兩邊![]() ,
,![]() 分別過點
分別過點![]() ,C,
,C,
∴OC=OB,OC⊥OB,
∵BC=2,
∴OC2=BC2-OB2,
2OC2=BC2,
2OC2=4,
即OC=![]() ;
;
(2)![]() ;
;
證明:如圖,連接![]() ,
,![]() ,
,

∵點![]() 是正方形
是正方形![]() 的兩條對角線的交點,
的兩條對角線的交點,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中 ,
,
∴![]() ,
,
∴![]() ;
;
(3)連接![]() ,
,![]() ,
,

∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】我們規定:相等的實數看作同一個實數.有下列六種說法:
①數軸上有無數多個表示無理數的點;
②帶根號的數不一定是無理數;
③每個有理數都可以用數軸上唯一的點來表示;
④數軸上每一個點都表示唯一一個實數;
⑤沒有最大的負實數,但有最小的正實數;
⑥沒有最大的正整數,但有最小的正整數.
其中說法錯誤的有_____(注:填寫出所有錯誤說法的編號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店準備購進A、B兩種型號的書包共50個進行銷售,兩種書包的進價、售價如下表所示:
書包型號 | 進價(元/個) | 售價(元/個) |
A型 | 200 | 300 |
B型 | 100 | 150 |
購進這50個書包的總費用不超過7300元,且購進B型書包的個數不大于A型書包個數的![]() .
.
(1)該文具店有哪幾種進貨方案?
(2)若該文具店購進的50個書包全部售完,則該文具店采用哪種進貨方案,才能獲得最大利潤?最大利潤是多少?(利潤=售價﹣進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,點O是對角線BD中點,點E在邊BC上,EO的延長線與邊AD交于點F,連接BF、DE,如圖1.

(1)求證:四邊形BEDF是平行四邊形;
(2)在(1)中,若DE=DC,∠CBD=45°,過點C作DE的垂線,與DE、BD、BF分別交于點G、H、R,如圖2.
①當CD=6,CE=4時,求BE的長.
②探究BH與AF的數量關系,并給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直角坐標系中,已知點P(-2,-1),點T(t,0)是x軸上的一個動點.

(1)求點P關于原點的對稱點P′的坐標;
(2)當t取何值時,△P′TO是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,攔水壩的橫斷面為等腰梯形ABCD,壩頂寬BC為6 m,壩高為3.2 m,為了提高水壩的攔水能力需要將水壩加高2 m,并且保持壩頂寬度不變,迎水坡CD的坡度不變,但是背水坡的坡度由原來的1∶2變成1∶2.5(坡度是坡高與坡的水平長度的比).求加高后的壩底HD的長為多少.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,把4個長為a,寬為b的長方形拼成如圖②所示的圖形,且a=3b,則根據這個圖形不能得到的等式是( )

A.(a+b)2=4ab+(a-b)2B.4b2+4ab=(a+b)2
C.(a-b)2=16b2-4abD.(a-b)2+12a2=(a+b)2
查看答案和解析>>
科目:初中數學 來源: 題型:
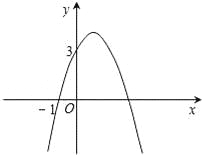
【題目】已知二次函數y=﹣x2+bx+c的圖象如圖所示,它與x軸的一個交點坐標為(﹣1,0),與y軸的交點坐標為(0,3).
(1)求出b,c的值,并寫出此二次函數的解析式;
(2)根據圖象,寫出函數值y為正數時,自變量x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com