
【題目】矩形![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() ),以
),以![]() 為旋轉中心順時針旋轉矩形
為旋轉中心順時針旋轉矩形![]() ,得到矩形
,得到矩形![]() .
.
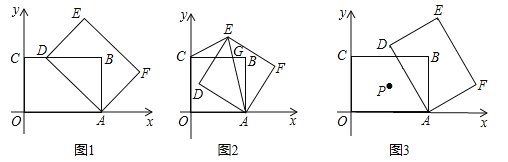
(1)如圖1,當點![]() 落在邊
落在邊![]() 上時,求
上時,求![]() 的長;
的長;
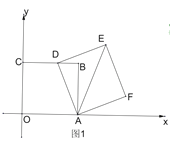
(2)如圖2,當![]() 時,矩形
時,矩形![]() 的對角線
的對角線![]() 交矩形
交矩形![]() 的邊
的邊![]() 于點
于點![]() ,連結
,連結![]() ,若
,若![]() 是等腰三角形,求直線
是等腰三角形,求直線![]() 的解析式.
的解析式.
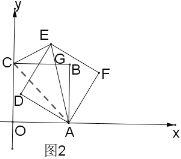
(3)如圖3,當![]() 時,矩形
時,矩形![]() 的對稱中心為點
的對稱中心為點![]() .
.![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)如圖1,當點D落在邊BC上時,BD2=AD2AB2,即可求解;
(2)分CG=EG、CE=GE、CE=CG三種情況分別求解;
(3)根據MN≤MA+AD,當射線DA經過點M時,MN=MA+AD=![]() ,
,![]() 的最大值是
的最大值是![]() ,當邊AD經過點M,即P與M重合時,MN=PD,MN=PD=ADAP=4
,當邊AD經過點M,即P與M重合時,MN=PD,MN=PD=ADAP=4![]() =
=![]() ,
,![]() 的最小值是
的最小值是![]() ,故可求解.
,故可求解.
解:(1) 如圖1,在矩形ABCO中,∠B =90°
當點D落在邊BC上時,BD2=AD2-AB2
∵C(0,3),A(![]() ,0)
,0)
∴AB=OC=3,AD=AO=![]()
∴![]()
(2) 如圖2, 連結AC,
∵![]() =3
=3
∴OA=OC=3
∴矩形ABCO是正方形
∴∠BCA =45°
設∠ECG的度數為![]() ,
,
∴AE=AC
∴∠AEC =∠ACE=![]()
①當CG=EG時,![]() =
=![]()
解得,不合題意,舍去
②當CE=GE時,∠ECG =∠EGC=![]()
∵∠ECG+∠EGC+∠CEG=![]()
∴![]() ,
,
解得![]()
∴∠AEC =∠ACE=![]() ,不合題意,舍去
,不合題意,舍去
③當CE=CG時,∠CEG =∠CGE=![]()
∵∠ECG+∠EGC+∠CEG=![]()
∴![]() ,
,
解得![]()
∴∠AEC =∠ACE=75°,∠CAE=30°
如圖3,連結OB,交AC于點Q,過E作EH⊥AC于H,連結BE
∴EH=![]() AE=
AE=![]() AC,BQ=
AC,BQ=![]() AC
AC
∴EH=BQ ,EH∥BQ且∠EHQ=90°
∴四邊形EHQB是矩形
∴BE∥AC
設直線BE的解析式為![]()
∵點B(3,3)在直線上
∴![]() 6
6
∴直線BE的解析式為![]() ;
;
(3)如圖4,∵![]() =4,點M是矩形ABCO的對稱中心
=4,點M是矩形ABCO的對稱中心
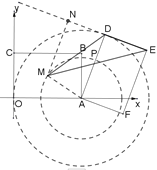
∴AO=4,AM=![]()
以A為圓心,分別以AO、AM為半徑作圓,AD交小圓于P,
過M作MN⊥ED于N
∴DE切大圓于D
∴MN≥PD
根據“垂線段最短”,MN≤MA+AD,
如圖5,當射線![]()
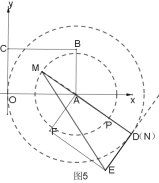
∴![]() 的最大值是
的最大值是![]()
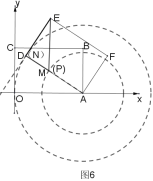
如圖6,當邊AD經過點M,即P與M重合時,MN=PD,
![]()
∴![]() 的最小值是
的最小值是![]()
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】八年級(1)班研究性學習小組為研究全校同學課外閱讀情況,在全校隨機邀請了部分同學參與問卷調查,統計同學們一個月閱讀課外書的數量,并繪制了以下統計圖.
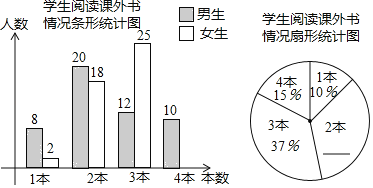
請根據圖中信息解決下列問題:
(1)共有多少名同學參與問卷調查;
(2)補全條形統計圖和扇形統計圖;
(3)全校共有學生1500人,請估計該校學生一個月閱讀2本課外書的人數約為多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的中線,點E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.
(1)求證:△AEF≌△DEB;
(2)若∠BAC=90°,求證:四邊形ADCF是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
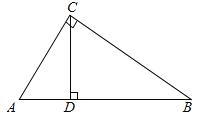
【題目】在△ABC中,∠C=90°,AC=3,BC=4,CD是斜邊AB上的高,點E在斜邊AB上,過點E作直線與△ABC的直角邊相交于點F,設AE=x,△AEF的面積為y.
(1)CD= ,AD= ;
(2)若EF⊥AB,當點E在線段AB上移動時;
①求y與x的函數關系式;(寫出自變量x的取值范圍)
②當x取何值時,y有最大值?并求其最大值
(3)若F在直角邊AC上(點F與A、C兩點均不重合),點E在斜邊AB上移動,試問:是否存在直線EF將△ABC的周長和面積同時平分?若存在直線EF,求出x的值;若不存在直線EF,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個正方形紙片AOBC放置在平面直角坐標系中,點A(0,4),點O(0,0),B(4,0),C(4,4)點.動點E在邊AO上,點F在邊BC上,沿EF折疊該紙片,使點O的對應點M始終落在邊AC上(點M不與A,C重合),點B落在點N處,MN與BC交于點P.
(Ⅰ)如圖①,當∠AEM=30°時,求點E的坐標;
(Ⅱ)如圖②,當點M落在AC的中點時,求點E的坐標;
(Ⅲ)隨著點M在AC邊上位置的變化,△MPC的周長是否發生變化?如變化,簡述理由;如不變,直接寫出其值.
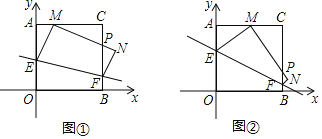
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖拋物線y=ax2+3ax+c(a>0)與y軸交于點C,與x軸交于A,B兩點,點A在點B左側.點B的坐標為(1,0),OC=3OB,

(1)求拋物線的解析式;
(2)若點D是線段AC下方拋物線上的動點,求四邊形ABCD面積的最大值;
(3)若點E在x軸上,點P在拋物線上.是否存在以A,C,E,P為頂點且以AC為一邊的平行四邊形?若存在,寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
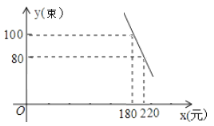
【題目】女本柔弱,為母則剛.說的是母親對子女無私的愛,母愛偉大.值此母親節來臨之際,某花店推出一款康乃馨花束,經過近幾年的市場調研發現,該花束在母親節的銷售量![]() (束)與銷售單價
(束)與銷售單價![]() (元)之間滿足如圖所示的一次函數關系,已知該花束的成本是每束
(元)之間滿足如圖所示的一次函數關系,已知該花束的成本是每束![]() 元.
元.
![]() 求出
求出![]() 關于
關于![]() 的函數關系式(不要求寫
的函數關系式(不要求寫![]() 的取值范圍);
的取值范圍);
![]() 設該花束在母親節盈利為
設該花束在母親節盈利為![]() 元,寫出
元,寫出![]() 關于
關于![]() 的函數關系式;并求出當售價定為多少元時,利潤最大;
的函數關系式;并求出當售價定為多少元時,利潤最大;
![]() 花店開拓新的進貨渠道,以降低成本,預計在今后的銷售中,母親節期間該花束的銷售量與銷售單價仍存在
花店開拓新的進貨渠道,以降低成本,預計在今后的銷售中,母親節期間該花束的銷售量與銷售單價仍存在![]() 中的關系若想實現銷售單價為
中的關系若想實現銷售單價為![]() 元,且銷售利潤不低于
元,且銷售利潤不低于![]() 元的銷售目標,該花束每束的成本應不超過多少元,
元的銷售目標,該花束每束的成本應不超過多少元,
查看答案和解析>>
科目:初中數學 來源: 題型:
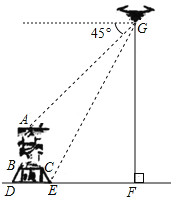
【題目】為了測量重慶有名的觀景點南山大金鷹的大致高度,小南同學使用的無人機進行觀察,當無人機與大金鷹側面在同一平面,且距離水平面垂直高度GF為100米時,小南調整攝像頭方向,當俯角為45°時,恰好可以拍攝到金鷹的頭頂A點;當俯角為63°時,恰好可以拍攝到金鷹底座點E.已知大金鷹是雄踞在一人造石臺上,石臺側面CE長12.5米,坡度為1:0.75,石臺上方BC長10米,頭部A點位于BC中點正上方.則金鷹自身高度約( )米.(結果保留一位小數,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com