
【題目】已知,如圖,二次函數![]() 圖像交
圖像交![]() 軸于
軸于![]() ,交
,交![]() 交軸于點
交軸于點![]() ,
,![]() 是拋物線的頂點,對稱軸
是拋物線的頂點,對稱軸![]() 經過
經過![]() 軸上的點
軸上的點![]() .
.
(1)求二次函數關系式;
(2)對稱軸![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 為對稱軸
為對稱軸![]() 上一動點.
上一動點.
①求![]() 的最小值及取得最小值時點
的最小值及取得最小值時點![]() 的坐標;
的坐標;
②在①的條件下,把![]() 沿著
沿著![]() 軸向右平移
軸向右平移![]() 個單位長度
個單位長度![]() 時,設
時,設![]() 與
與![]() 重疊部分面積記為
重疊部分面積記為![]() ,求
,求![]() 與
與![]() 之間的函數表達式,并求出
之間的函數表達式,并求出![]() 的最大值.
的最大值.
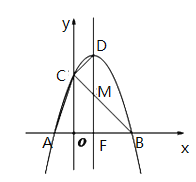
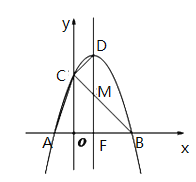
【答案】(1)![]() ;(2)①最小值為
;(2)①最小值為![]() ,點
,點![]() 坐標為
坐標為![]() ;②
;②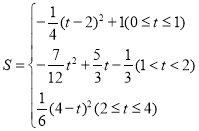 ,當
,當![]() 時,
時,![]() 最大值
最大值![]() .
.
【解析】
(1)函數對稱軸為x=1,則點B(3,0),用交點式表達式得:y=a(x+1)(x-3)=a(x2-2x-3),即可求解;
(2)①連接BD,過點A作AH⊥BD于點H,交DF于點P,AP+![]() PD=AP+PD,此時AP+
PD=AP+PD,此時AP+![]() PD=AH最小,即可求解;
PD=AH最小,即可求解;
②根據題意,可分為0≤t≤1、1<t<2、2≤t≤4三種情況,分別求解,即可得到答案.
解:(1)二次函數![]() 對稱軸為
對稱軸為![]() ,點
,點![]() 坐標為
坐標為![]() ,
,
則點![]() 坐標為
坐標為![]() .
.
又∵點![]() 坐標
坐標![]() ,則
,則
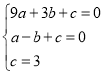 ,解得:
,解得: ,
,
∴函數表達式為![]() ;
;
(2)①連接![]()
∵![]()
∴![]()
在![]() 中,依勾股定理得:
中,依勾股定理得:![]()
∴![]()
過點![]() 作
作![]() 于點
于點![]() ,交拋物線對稱軸于點
,交拋物線對稱軸于點![]()
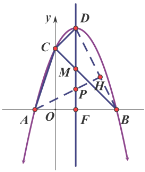
則![]()
則![]()
依“垂線段最短”得此時![]() 長度為最小值,
長度為最小值,
即![]() 最小值為
最小值為![]() 的長度,
的長度,
∵![]()
則![]() ,
,![]()
即![]() 最小值為
最小值為![]() .
.
點![]() 坐標為
坐標為![]() .
.
②A.當![]() 時,如圖
時,如圖
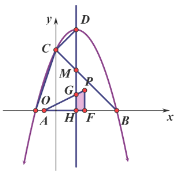
依圖知:![]()
則:![]()
![]()
化簡得:![]()
配方得:![]()
根據自變量取值范圍,當![]() 時,
時,![]() 最大值
最大值![]() 4
4
B.當![]() 時,如圖:
時,如圖:

![]() 四邊形
四邊形![]()
![]()
整理得:![]()
配方得:![]()
即![]() 時,
時,![]() 最大值
最大值![]()
C.當![]() 時,如圖:
時,如圖:
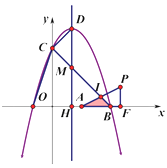
![]()
根據自變量取值范圍,當![]() 時,
時,![]() 最大值
最大值![]()
綜上,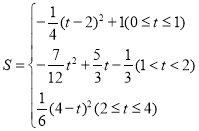 ,當
,當![]() 時,
時,![]() 最大值
最大值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,一艘輪船從位于燈塔C的北偏東方向,距離燈塔60海里的小島A出發,沿正南方向航行一段時間后,到達位于燈塔C的南偏東方向上的B處,這時輪船B與小島A的距離是( )
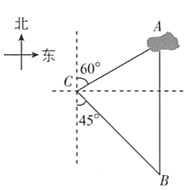
A.![]() 海里B.
海里B.![]() 海里C.120海里D.60海里
海里C.120海里D.60海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究:
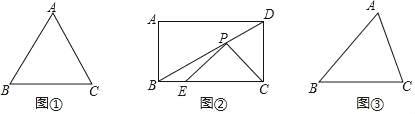
(1)如圖①,已知等邊△ABC,邊長為4,則△ABC的外接圓的半徑長為 .
(2)如圖②,在矩形ABCD中,AB=4,對角線BD與邊BC的夾角為30°,點E在為邊BC上且BE=![]() BC,點P是對角線BD上的一個動點,連接PE,PC,求△PEC周長的最小值.
BC,點P是對角線BD上的一個動點,連接PE,PC,求△PEC周長的最小值.
問題解決:
(3)為了迎接新年的到來,西安城墻舉辦了迎新年大型燈光秀表演.其中一個鐳射燈距城墻30米,鐳射燈發出的兩根彩色光線夾角為60°,如圖③,若將兩根光線(AB,AC)和光線與城墻的兩交點的連接的線段(BC)看作一個三角形,記為△ABC,那么該三角形周長有沒有最小值?若有,求出最小值,若沒有,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
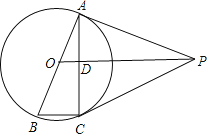
【題目】如圖,AB是⊙O的直徑,AC是弦,OD⊥AC于點D,過點A作⊙O的切線AP,AP與OD的延長線交于點P,連接PC、BC.
【1】猜想:線段OD與BC有何數量和位置關系,并證明你的結論.
【2】求證:PC是⊙O的切線
查看答案和解析>>
科目:初中數學 來源: 題型:
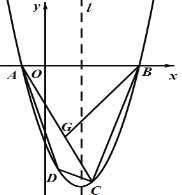
【題目】如圖,已知二次函數![]() 的圖象M經過
的圖象M經過![]() (
(![]() ,0),
,0),![]() (2,
(2,![]() )兩點且與
)兩點且與![]() 軸的另一個交點為
軸的另一個交點為![]() .
.
(1)求該二次函數的解析式;
(2)點![]() 是線段
是線段![]() 上的動點(點G與線段
上的動點(點G與線段![]() 的端點不重合),若△AGB∽△ABC,求點G的坐標;
的端點不重合),若△AGB∽△ABC,求點G的坐標;
(3)設拋物線的對稱軸為![]() ,點
,點![]()
![]() 是拋物線上一動點,當△ACD的面積為
是拋物線上一動點,當△ACD的面積為![]() 時,點D關于
時,點D關于![]() 的對稱點為E,能否在拋物線和
的對稱點為E,能否在拋物線和![]() 上分別找到點P、Q,使得以點D、E、P、Q為頂點的四邊形為平行四邊形. 若能,求出點P的坐標;若不能,請說明理由.
上分別找到點P、Q,使得以點D、E、P、Q為頂點的四邊形為平行四邊形. 若能,求出點P的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國“蛟龍”號深潛器目前最大深潛極限為7062.68米.某天該深潛器在海面下1800米處作業(如圖),測得正前方海底沉船C的俯角為45°,該深潛器在同一深度向正前方直線航行2000米到B點,此時測得海底沉船C的俯角為60°.請判斷沉船C是否在“蛟龍”號深潛極限范圍內?并說明理由;(精確到0.01)(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,過點
,過點![]() 作
作![]() 的平行線與
的平行線與![]() 的平分線交于點
的平分線交于點![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 是菱形;
是菱形;
(2)連接![]() 與
與![]() 交于點
交于點![]() ,過點
,過點![]() 作
作![]() 的延長線交于
的延長線交于![]() 點,連接
點,連接![]() ,若
,若![]() ,
,![]() ,直接寫出
,直接寫出![]() 的長為 .
的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
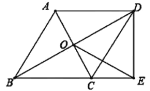
【題目】如圖,四邊形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分別以點A,C為圓心,大于![]() AC長為半徑作弧,兩弧交于點E,射線BE交AD于點F,交AC于點O.若點O恰好是AC的中點,則CD的長為__.
AC長為半徑作弧,兩弧交于點E,射線BE交AD于點F,交AC于點O.若點O恰好是AC的中點,則CD的長為__.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com