
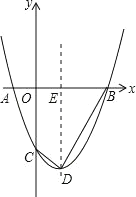
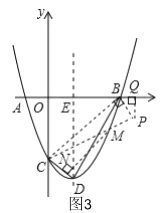
【題目】如圖,已知:拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于點C,點D為頂點,連接BD,CD,拋物線的對稱軸與x軸交與點E.
(1)求拋物線解析式及點D的坐標;
(2)G是拋物線上B,D之間的一點,且S四邊形CDGB=4S△DGB,求出G點坐標;
(3)在拋物線上B,D之間是否存在一點M,過點M作MN⊥CD,交直線CD于點N,使以C,M,N為頂點的三角形與△BDE相似?若存在,求出滿足條件的點M的坐標,若不存在,請說明理由.
【答案】(1)![]() ;頂點
;頂點![]()
![]() ;(2)
;(2)![]() ;(3)存在,點
;(3)存在,點![]() 或
或![]() .
.
【解析】
(1)利用待定系數法可求得拋物線的解析式,然后化成頂點式可得點D的坐標;
(2)連接BC,BG,DG,首先求出![]() ,然后根據S四邊形CDGB=4S△DGB可得
,然后根據S四邊形CDGB=4S△DGB可得![]() ,求出直線
,求出直線![]() 的解析式,設
的解析式,設![]() ,則H(x,2x-6),根據
,則H(x,2x-6),根據![]() 得出方程,解方程求出x即可解決問題;
得出方程,解方程求出x即可解決問題;
(3)如圖3,以C,M,N為頂點的三角形與△BDE相似,則以B,C,P為頂點的三角形與△BDE相似,則![]() 或
或![]() ,求出
,求出![]() 或
或![]() ;然后分
;然后分![]() 和
和![]() 兩種情況,分別求出直線CP的解析式即可解決問題.
兩種情況,分別求出直線CP的解析式即可解決問題.
解:(1)![]() 拋物線
拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,
兩點,
![]() ,解得
,解得![]() ,
,
∴拋物線的解析式為:![]() ;
;
![]() ,
,
![]() 頂點
頂點![]() 的坐標為
的坐標為![]() ;
;
(2)如圖2,連接![]() ,BG,DG,
,BG,DG,
在![]() 中,令
中,令![]() ,則
,則![]() ,
,
∴點![]() ,
,
∴易求直線![]() 的解析式為
的解析式為![]() ,
,
設直線![]() 與對稱軸相交于點
與對稱軸相交于點![]() ,
,
當![]() 時,
時,![]() ,
,
∴點![]() ,
,
∴![]() ,
,
![]() ,
,
![]() 四邊形
四邊形![]() ,
,
![]() ,
,
設過點![]() 與
與![]() 軸平行的直線交BD于點
軸平行的直線交BD于點![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,
,
則![]() ,解得
,解得![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
設![]() ,則H(x,2x-6),
,則H(x,2x-6),
∴![]() ,
,
∴![]() ,
,
整理得,![]() ,
,
解得:![]() ,則
,則![]() ,
,
∴點![]() ;
;
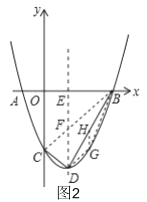
(3)存在,
由勾股定理得,![]() ,
,
如圖3,過點![]() 作
作![]() 交
交![]() 的延長線于
的延長線于![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() 與
與![]() 軸的夾角都是
軸的夾角都是![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() 以
以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,
相似,
![]() 以
以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,
相似,
![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
解得:![]() 或
或![]() ,
,
過點![]() 作
作![]() 軸于
軸于![]() ,
,
![]() ,
,
![]() ,
,
①當![]() 時,
時,![]() ,
,
∴![]() ,
,
∴點![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,
,
則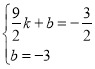 ,解得
,解得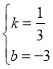 ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
聯立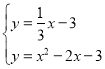 ,解得:
,解得: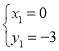 (舍去),
(舍去),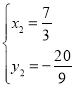 ,
,
∴點![]() ;
;
②當![]() 時,
時,![]() ,
,
∴![]() ,
,
∴點![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,
,
則![]() ,解得
,解得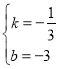 ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
聯立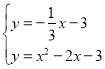 ,解得
,解得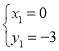 (舍去),
(舍去),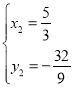 ,
,
![]() 點
點![]() ,
,
綜上所述,存在點![]() 或
或![]() ,使以
,使以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
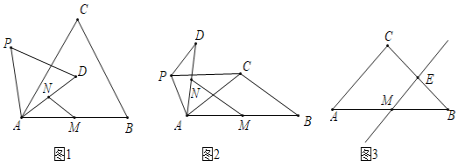
【題目】在△ABC中,CA=CB,∠ACB=α(0°<α<180°).點P是平面內不與A,C重合的任意一點,連接AP,將線段AP繞點P逆時針旋轉α得到線段DP,連接AD,CP.點M是AB的中點,點N是AD的中點.
(1)問題發現:如圖1,當α=60°時,![]() 的值是 ,直線MN與直線PC相交所成的較小角的度數是 .
的值是 ,直線MN與直線PC相交所成的較小角的度數是 .
(2)類比探究:如圖2,當α=120°時,請寫出的![]() 值及直線MN與直線PC相交所成的較小角的度數,并就圖2的情形說明理由.
值及直線MN與直線PC相交所成的較小角的度數,并就圖2的情形說明理由.
(3)解決問題:如圖3,當α=90°時,若點E是CB的中點,點P在直線ME上,請直接寫出點B,P,D在同一條直線上時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C = 90°,點O是斜邊AB上一定點,到點O的距離等于OB的所有點組成圖形W,圖形W與AB,BC分別交于點D,E,連接AE,DE,∠AED=∠B.

(1)判斷圖形W與AE所在直線的公共點個數,并證明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直線l上,將△ABC繞點A順時針旋轉到①,可得到點P1,此時AP1=2;將位置①的三角形繞點P1順時針旋轉到位置②,可得到點P2,此時AP2=2+![]() ;將位置②的三角形繞點P2順時針旋轉到位置③,可得到點P3,此時AP3=3+
;將位置②的三角形繞點P2順時針旋轉到位置③,可得到點P3,此時AP3=3+![]() ;…按此規律繼續旋轉,直到點P2020為止,則AP2020等于_______.
;…按此規律繼續旋轉,直到點P2020為止,則AP2020等于_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.五張完全相同的卡片上,分別畫有圓、平行四邊形、等邊三角形、角、線段,現從中隨機抽取一張,恰好抽到軸對稱圖形的概率是![]()
B.事件“任意畫一個多邊形,其外角和是![]() ”是必然事件
”是必然事件
C.一個盒子中有白球![]() 個,紅球
個,紅球![]() 個,黑球
個,黑球![]() 個(每個除了顏色外都相同).如果從中任取一個球,取得的是紅球的概率與不是紅球的概率相同,那么
個(每個除了顏色外都相同).如果從中任取一個球,取得的是紅球的概率與不是紅球的概率相同,那么![]() 與
與![]() 的差是
的差是![]()
D.事件“把![]() 個球放入三個抽屜中,其中一個抽屜中至少有
個球放入三個抽屜中,其中一個抽屜中至少有![]() 個球”是隨機事件
個球”是隨機事件
查看答案和解析>>
科目:初中數學 來源: 題型:
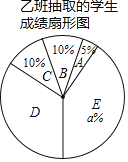
【題目】入學考試前,某語文老師為了了解所任教的甲、乙兩班學生假期向的語文基礎知識背誦情況,對兩個班的學生進行了語文基礎知識背誦檢測,滿分100分.現從兩個班分別隨機抽取了20名學生的檢測成績進行整理,描述和分析(成績得分用x表示,共分為五組:
A.0≤x<80,B.80≤x<85,C.85≤x<90,D.90≤x<95,E.95≤x<100),下面給出了部分信息:
甲班20名學生的成績為:
甲組 | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
乙班20名學生的成績在D組中的數據是:93,91,92,94,92,92,92
甲、乙兩班抽取的學生成績數據統計表
班級 | 甲組 | 乙組 |
平均數 | 91 | 92 |
中位數 | 91 | b |
眾數 | c | 92 |
方差 | 41.2 | 27.3 |
根據以上信息,解答下列問題:
(1)直接寫出上述圖表中a,b,c的值:a= ;b= ;c= ;
(2)根據以上數據,你認為甲、乙兩個班中哪個班的學生基礎知識背誦情況較好?請說明理由(一條理由即可);
(3)若甲、乙兩班總人數為125,且都參加了此次基礎知識檢測,估計此次檢測成績優秀(x≥95)的學生人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
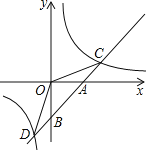
【題目】如圖,直線y=kx+b與x軸交于點A,與y軸交于點B,OB=4,sin∠CBO=![]() .
.
(1)求直線AB的解析式;
(2)直線AB與反比例函數y=![]() 相交于C、D兩點(C點在第一象限),求S△DOC的面積.
相交于C、D兩點(C點在第一象限),求S△DOC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com