
【題目】在△ABC中,AB=AC,BD⊥AC于D,若cos∠BAD=![]() ,BD=
,BD=![]() ,則CD的長為__________.
,則CD的長為__________.
【答案】1或5
【解析】
分兩種情況:①若△ABC為銳角三角形,在Rt△ABD中由cos∠BAD=![]() ,可設AD=2x,AB=3x,結合BD的長根據勾股定理列方程,求得x的值后即可得AB=AC=3,AD=2,由CD=ACAD得出答案;②若△ABC為鈍角三角形,同理可得AD=2,AB=AC=3,由CD=AC+AD得出答案.
,可設AD=2x,AB=3x,結合BD的長根據勾股定理列方程,求得x的值后即可得AB=AC=3,AD=2,由CD=ACAD得出答案;②若△ABC為鈍角三角形,同理可得AD=2,AB=AC=3,由CD=AC+AD得出答案.
解:①如圖1,若△ABC為銳角三角形,
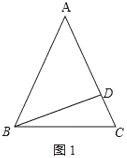
∵BD⊥AC,
∴∠ADB=90°,
∵cos∠BAD=![]() ,
,
∴設AD=2x,AB=3x,
∵AB2=AD2+BD2,
∴9x2=4x2+5,
解得:x=1或x=1(舍),
∴AB=AC=3x=3,AD=2x=2,
∴CD=ACAD=1;
②如圖2,若△ABC為鈍角三角形,
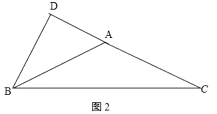
同理可得,AD=2,AB=AC=3,
∴CD=AC+AD=5,
故答案為:1或5.


科目:初中數學 來源: 題型:
【題目】如圖,⊙O中,AC為直徑,MA,MB分別切⊙O于點A,B,∠BAC=25°,則∠AMB的大小為( )
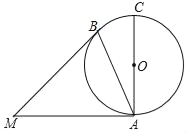
A. 25°B. 30°C. 45°D. 50°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了了解“校園文明監督崗”的值圍情況,對全校各班級進行了抽樣調查,過程如下:
收集數據:從三個年級中隨機抽取了20個班級,學校對各班的評分如下:
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述數據:按如下分數段整理、描述這兩組樣本數據:
分數段 |
|
|
|
|
|
班級數 | 1 | 2 | a | 8 | b |
![]() 說明:成績90分及以上為優秀,
說明:成績90分及以上為優秀,![]() 分為良好,
分為良好,![]() 分為合格,60分以下為不合格
分為合格,60分以下為不合格![]()
分析數據:樣本數據的平均數、中位數、眾數、極差如下表,繪制扇形統計圖:
平均數 | 中位數 | 眾數 | 極差 |
79 | c | 82 | d |
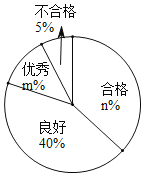
請根據以上信息解答下列問題:
![]() 填空:
填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 若我校共120個班級,估計得分為優秀的班級有多少個?
若我校共120個班級,估計得分為優秀的班級有多少個?
![]() 為調動班級積極性,決定制定一個獎勵標準分,凡到達或超過這個標準分的班級都將受到獎勵
為調動班級積極性,決定制定一個獎勵標準分,凡到達或超過這個標準分的班級都將受到獎勵![]() 如果要使得半數左右的班級都能獲獎,獎勵標準分應定為多少分?并簡述其理由
如果要使得半數左右的班級都能獲獎,獎勵標準分應定為多少分?并簡述其理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=∠DCB,添加以下條件,不能判定△ABC≌△DCB的是( )
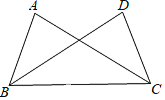
A.∠A=∠DB.∠ACB=∠DBCC.AC=DBD.AB=DC
查看答案和解析>>
科目:初中數學 來源: 題型:
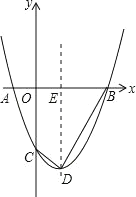
【題目】如圖,已知:拋物線y=x2+bx+c與x軸交于A(﹣1,0),B(3,0)兩點,與y軸交于點C,點D為頂點,連接BD,CD,拋物線的對稱軸與x軸交與點E.
(1)求拋物線解析式及點D的坐標;
(2)G是拋物線上B,D之間的一點,且S四邊形CDGB=4S△DGB,求出G點坐標;
(3)在拋物線上B,D之間是否存在一點M,過點M作MN⊥CD,交直線CD于點N,使以C,M,N為頂點的三角形與△BDE相似?若存在,求出滿足條件的點M的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
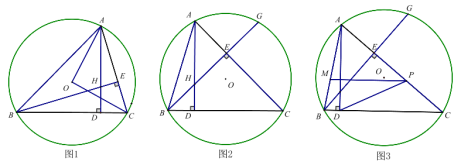
【題目】已知,△ABC內接于⊙O,AD⊥BC于D,BE⊥AC于E,AD、BE交于點H.
(1)如圖1,連接OA、OC,若BH=AC,求∠AOC的度數.
(2)如圖2延長BE交⊙O于點G,求證:HE=GE;
(3)如圖3,在(2)的條件下,P是弦AC上一點,過點P作PM∥BC交AB于點M,若∠PCD+2∠PDC=90°,BM=![]() ,AM=
,AM=![]() ,求⊙O半徑.
,求⊙O半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在矩形![]() 中,,
中,,![]() 以邊
以邊![]() 所在的直線為軸建立平面直角坐標系
所在的直線為軸建立平面直角坐標系![]() ,反比例函數
,反比例函數![]() 的圖象經過點
的圖象經過點![]() ,點
,點![]() 是
是![]() 軸正半軸上的動點,將點
軸正半軸上的動點,將點![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() ,使點
,使點![]() 恰好落在反比例
恰好落在反比例![]() 的圖象上,則
的圖象上,則![]() 的值是__________.
的值是__________.
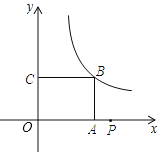
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線![]() :
:![]() 與直線
與直線![]() :
:![]() 交于點
交于點![]() ,且
,且![]() .
.
(1)若![]() 是第二象限位于直線
是第二象限位于直線![]() 上方的一點,過
上方的一點,過![]() 作
作![]() 于
于![]() ,過
,過![]() 作
作![]() 軸交直線
軸交直線![]() 于
于![]() ,
,![]() 為
為![]() 中點,其中
中點,其中![]() 的周長是
的周長是![]() ,若
,若![]() 為線段
為線段![]() 上一動點,連接
上一動點,連接![]() ,求
,求![]() 的最小值,此時
的最小值,此時![]() 軸上有一個動點
軸上有一個動點![]() ,當
,當![]() 最大時,求
最大時,求![]() 點坐標;
點坐標;
(2)在(1)的情況下,將![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() 后得到
后得到![]() ,如圖2,將線段
,如圖2,將線段![]() 沿著
沿著![]() 軸平移,記平移過程中的線段
軸平移,記平移過程中的線段![]() 為
為![]() ,在平面直角坐標系中是否存在點
,在平面直角坐標系中是否存在點![]() ,使得以點
,使得以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形為菱形,若存在,請求出點
為頂點的四邊形為菱形,若存在,請求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
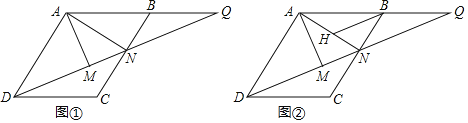
【題目】已知平行四邊形ABCD中,N是邊BC上一點,延長DN、AB交于點Q,過A作AM⊥DN于點M,連接AN,則AD⊥AN.
(1)如圖①,若tan∠ADM=![]() ,MN=3,求BC的長;
,MN=3,求BC的長;
(2)如圖②,過點B作BH∥DQ交AN于點H,若AM=CN,求證:DM=BH+NH.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com