Question

【題目】如圖所示，在平面直角坐標系中，一次函數與反比例函數交于、兩點，與軸交于點，作軸，垂足為，已知，．

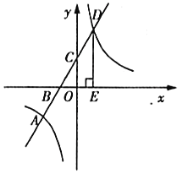
（1）求一次函數與反比例函數的解析式；

（2）連接、，在軸取點，使與面積相等，求點坐標．

Answer 1

【答案】（1）；；（2）（2,0）或（-4,0）.

【解析】

（1）根據題意，結合直角三角形求解，得出點B、C的坐標代入一次函數，可得直線解析式，進而求出點D，可求出反比例函數的解析式即可；

（2）聯立方程組求出點A，進而求出的面積，根據與面積相等列出關于底邊長的一次方程求解即可．

（1）在Rt△COB中，OB=1，，

∴CO=，

將點B（-1，0），點C（0，）代入，得

，

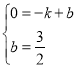解得，

∴，

∵CO⊥x軸，DE⊥x軸，OB=OE，

∴CO為△BED的中位線，

∴DE=2CO=3，

∴點D的坐標為（1，3），

∴將（1，3）代入，得m=3，

∴，

故答案為：；；

（2）連接DO、AO，

將與聯立方程組，得

，

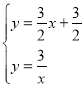解得或，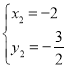

∴點A坐標為（-2，），D（1,3），

∴，

設△CBF的底邊長為a，

可得：，

解得：a=3，

∴點F的坐標為（-1+3，0），（-1-3，0），

即點F的坐標為（2，0）或（-4，0），

故答案為：（2，0）或（-4，0）．