
5.解:由題意得 z1=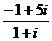 =2+3i,
=2+3i,
于是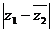 =
=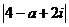 =
= ,
,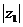 =
=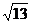 .
.
 <
<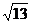 ,
,
得a2-8a+7<0,1<a<7.
4.解: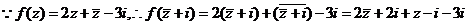
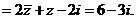
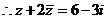 。
。
設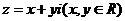 ,則
,則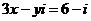
從而有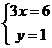 ,即
,即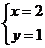 ,
,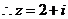 .
.
所以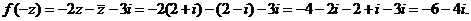
3. 解:∵|z1|>|z2|,∴x4+x2+1>(x2+a)2
∴(1-2a)x2+(1-a2)>0對x∈R恒成立
當1-2a=0,即a=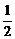 時,不等式成立;
時,不等式成立;
當1-2a≠0時,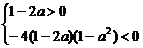
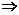 -1<a<
-1<a<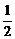

綜上,a∈(-1,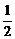 ]
]
2.解法一:設z=a+bi(a,b∈R),則(1+3i)z=a-3b+(3a+b)i.
由題意,得a=3b≠0.∵|ω|=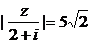 ,∴|z|=
,∴|z|=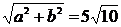 .
.
將a=3b代入,解得a=±15,b=±15.故ω=±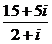 =±(7-i).
=±(7-i).
解法二:由題意,設(1+3i)z=ki,k≠0且k∈R,則ω=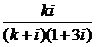 .
.
∵|ω|=5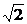 ,∴k=±50.故ω=±(7-i).
,∴k=±50.故ω=±(7-i).
1.解:(1)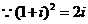 ,令
,令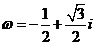 ,則
,則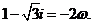
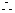
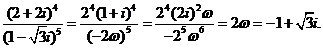
(2)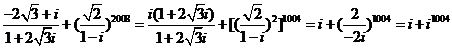
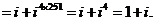
1.A 2.B 3.A 4.C 5.-4 6.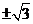
[典例精析]
變式訓練:
5.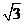
[基礎闖關]
4.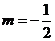
3.(1)一次因式 共軛復數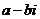
2.(1)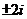
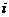
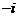 (2)1 0 0
(2)1 0 0
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com