
2.(2009全國卷Ⅰ理)本小題滿分12分。(注意:在試題卷上作答無效)
設函數 在兩個極值點
在兩個極值點 ,且
,且
(I)求 滿足的約束條件,并在下面的坐標平面內,畫出滿足這些條件的點
滿足的約束條件,并在下面的坐標平面內,畫出滿足這些條件的點 的區域;
的區域;
(II)證明:
 分析(I)這一問主要考查了二次函數根的分布及線性規劃作可行域的能力。
分析(I)這一問主要考查了二次函數根的分布及線性規劃作可行域的能力。
大部分考生有思路并能夠得分。 由題意知方程
由題意知方程 有兩個根
有兩個根


 則有
則有

 故有
故有
 右圖中陰影部分即是滿足這些條件的點
右圖中陰影部分即是滿足這些條件的點 的區域。
的區域。
(II)這一問考生不易得分,有一定的區分度。主要原因是含字母較多,不易找到突破口。此題主要利用消元的手段,消去目標 中的
中的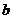 ,(如果消
,(如果消 會較繁瑣)再利用
會較繁瑣)再利用 的范圍,并借助(I)中的約束條件得
的范圍,并借助(I)中的約束條件得 進而求解,有較強的技巧性。
進而求解,有較強的技巧性。
解: 由題意有 ............①
............①
又 .....................②
.....................②
消去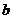 可得
可得 .
.
又 ,且
,且

1.(2009年廣東卷文)(本小題滿分14分)
已知二次函數 的導函數的圖像與直線
的導函數的圖像與直線 平行,且
平行,且 在
在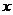 =-1處取得最小值m-1(m
=-1處取得最小值m-1(m ).設函數
).設函數
(1)若曲線 上的點P到點Q(0,2)的距離的最小值為
上的點P到點Q(0,2)的距離的最小值為 ,求m的值
,求m的值
(2)  如何取值時,函數
如何取值時,函數 存在零點,并求出零點.
存在零點,并求出零點.
[解析](1)設 ,則
,則 ;
;
又 的圖像與直線
的圖像與直線 平行
平行 
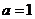
又 在
在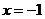 取極小值,
取極小值,  ,
, 
 ,
,  ;
;
 , 設
, 設
則


 ;21世紀教育網
;21世紀教育網
(2)由 ,
,
得 

當 時,方程
時,方程 有一解
有一解 ,函數
,函數 有一零點
有一零點 ;
;
當 時,方程
時,方程 有二解
有二解 ,若
,若 ,
, ,
,
函數 有兩個零點
有兩個零點 ;若
;若 ,
,
 ,函數
,函數 有兩個零點
有兩個零點 ;
;
當 時,方程
時,方程 有一解
有一解 ,
,  ,
函數
,
函數 有一零點
有一零點 21世紀教育網
21世紀教育網
19.(2009重慶卷文)記 的反函數為
的反函數為 ,則方程
,則方程 的解
的解 .
.
[答案]2
解法1由 ,得
,得 ,即
,即 ,于是由
,于是由 ,解得
,解得
解法2因為 ,所以
,所以
18.(2009寧夏海南卷文)曲線 在點(0,1)處的切線方程為
。
在點(0,1)處的切線方程為
。
[答案]
[解析] ,斜率k=
,斜率k= =3,所以,y-1=3x,即
=3,所以,y-1=3x,即
16.(2009陜西卷理)設曲線 在點(1,1)處的切線與x軸的交點的橫坐標為
在點(1,1)處的切線與x軸的交點的橫坐標為 ,令
,令 ,則
,則 的值為
.
的值為
.
答案:-2

15.(2009福建卷理)若曲線 存在垂直于
存在垂直于 軸的切線,則實數
軸的切線,則實數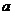 取值范圍是_____________.
取值范圍是_____________.
[答案]:
解析:由題意可知 ,又因為存在垂直于
,又因為存在垂直于 軸的切線,
軸的切線,
所以 。
。
13.(2009山東卷文)若函數f(x)=a -x-a(a>0且a
-x-a(a>0且a 1)有兩個零點,則實數a的取值范圍是 .
1)有兩個零點,則實數a的取值范圍是 .
[解析]: 設函數 且
且 和函數
和函數 ,則函數f(x)=a
,則函數f(x)=a -x-a(a>0且a
-x-a(a>0且a 1)有兩個零點, 就是函數
1)有兩個零點, 就是函數 且
且 與函數
與函數 有兩個交點,由圖象可知當
有兩個交點,由圖象可知當 時兩函數只有一個交點,不符合,當
時兩函數只有一個交點,不符合,當 時,因為函數
時,因為函數 的圖象過點(0,1),而直線
的圖象過點(0,1),而直線 所過的點(0,a)一定在點(0,1)的上方,所以一定有兩個交點.所以實數a的取值范圍是
所過的點(0,a)一定在點(0,1)的上方,所以一定有兩個交點.所以實數a的取值范圍是 .
.
答案: 
[命題立意]:本題考查了指數函數的圖象與直線的位置關系,隱含著對指數函數的性質的考查,根據其底數的不同取值范圍而分別畫出函數的圖象進行解答.
12.(2009山東卷理)已知定義在R上的奇函數 ,滿足
,滿足 ,且在區間[0,2]上是增函數,若方程f(x)=m(m>0)在區間
,且在區間[0,2]上是增函數,若方程f(x)=m(m>0)在區間 上有四個不同的根
上有四個不同的根 ,則
,則
[解析]:因為定義在R上的奇函數,滿足 ,所以
,所以 ,所以, 由
,所以, 由 為奇函數,所以函數圖象關于直線
為奇函數,所以函數圖象關于直線 對稱且
對稱且 ,由
,由 知
知 ,所以函數是以8為周期的周期函數,又因為
,所以函數是以8為周期的周期函數,又因為 在區間[0,2]上是增函數,所以
在區間[0,2]上是增函數,所以 在區間[-2,0]上也是增函數.如圖所示,那么方程f(x)=m(m>0)在區間
在區間[-2,0]上也是增函數.如圖所示,那么方程f(x)=m(m>0)在區間 上有四個不同的根
上有四個不同的根 ,不妨設
,不妨設 由對稱性知
由對稱性知
 所以
所以
 答案:-8
答案:-8
[命題立意]:本題綜合考查了函數的奇偶性,單調性,
對稱性,周期性,以及由函數圖象解答方程問題,
運用數形結合的思想和函數與方程的思想解答問題.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com