
回歸卷之三角函數――必修四、五
一、三角函數的定義
1、已知 ,在終邊
,在終邊 上取異于原點O的點P,則
上取異于原點O的點P,則 ______________.
______________.
2、已知 ,
, 在第三象限,
在第三象限, ______________.
______________.
3、在復平面內,O為坐標原點, 對應的復數為3+4i,
對應的復數為3+4i, 繞著O逆時針方向旋轉
繞著O逆時針方向旋轉 得到向量
得到向量 ,此向量對應復數是( )
,此向量對應復數是( )
4、必修四P126――3 , P25――4
二、平方關系
1、如果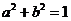 ,求
,求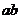 的范圍______________,
的范圍______________,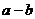 的范圍_________________,
的范圍_________________,
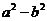 的范圍______________,
的范圍______________,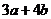 的范圍______________.
的范圍______________.
2、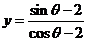 的值域______________
的值域______________
3、已知 ,求
,求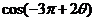 =______________
=______________
4、曲線C的參數方程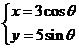 ,P(x,y)為C上的任意一點,A(0,-4),B(0,4)則
,P(x,y)為C上的任意一點,A(0,-4),B(0,4)則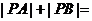 ______________.
______________.
5、必修四P157――B組5
三、三角變換
1、理清公式之間聯系,P153――例2
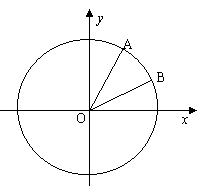 2、必修五P9――解三角形的進一步討論;P11B組――1 P21練習3
2、必修五P9――解三角形的進一步討論;P11B組――1 P21練習3
四、基本題型
1、如圖,在平面直角坐標系xoy中,以ox軸為始邊做兩個銳角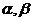 ,它們的終邊分別與單位圓相交于A、B兩點,已知A、B的橫坐標分別為
,它們的終邊分別與單位圓相交于A、B兩點,已知A、B的橫坐標分別為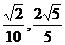
(1)求 的值; (2)求
的值; (2)求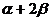 的值。
的值。
2、如圖,已知點 點
點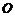 為坐標原點,點
為坐標原點,點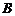 在第二象限,且
在第二象限,且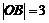 ,記
,記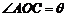 .
. 學科網
學科網
 (Ⅰ)求
(Ⅰ)求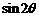 的值;
的值; 學科網 (Ⅱ)若
學科網 (Ⅱ)若 學科
學科 ,求
,求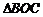 的面積.
的面積.
3、已知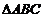 中,
中,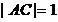 ,
,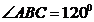 ,
,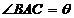 ,記
,記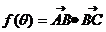 ,
,
(1)求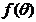 關于
關于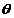 的表達式;(2)求
的表達式;(2)求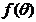 的值域;
的值域;
4、.若sinx+siny=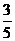 ,cosx+cosy=
,cosx+cosy=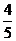
(1)求cos(x+y)的值;
(2)求cosx?cosy的值。
答案:四:1 (1)-3 (2)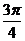 2(1)
2(1)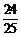 (2)
(2)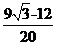 3 (2)
3 (2)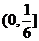
4 (1)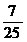 (2)-
(2)-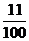
回歸卷之平面向量(必修四)
一、回答下列式子的幾何意義
1、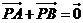
2、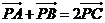
3、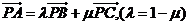
4、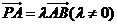
5、在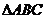 中,
中,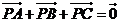
6、在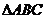 中,
中,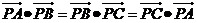
7、在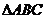 中,
中,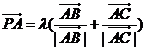
8、四邊形ABCD,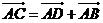
9、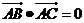
10、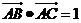
11、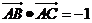
二、兩個向量的數量積與兩個向量共線
1、兩個向量夾角的取值范圍______________。在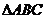 中,A、B、C成等差數列,
中,A、B、C成等差數列,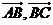 的夾角是______________。
的夾角是______________。
2、已知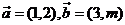
①如果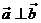 ,m=( ), ②如果
,m=( ), ②如果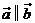 ,m=( )
,m=( )
③如果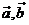 的夾角為銳角,m的范圍是( ) ④如果
的夾角為銳角,m的范圍是( ) ④如果 ,m=( )
,m=( )
⑤如果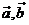 可作為平面向量的基底,m的范圍是( )
可作為平面向量的基底,m的范圍是( )
⑥與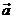 垂直的單位向量的坐標是______________.
垂直的單位向量的坐標是______________.
3、已知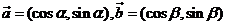 ①如果
①如果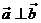 ,
,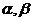 的關系是___________。②如果
的關系是___________。②如果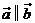 ,
,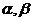 的關系是______________。
的關系是______________。
③如果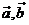 的夾角為
的夾角為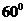 ,
,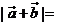 ( ),
( ),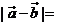 ( ),直線
( ),直線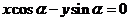 與圓
與圓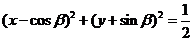 的位置關系是( )
的位置關系是( )
課本必修四P151B組4, P157B組4,P120,4
三、基本題型
1、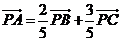 ,
,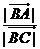 =______________.
=______________.
2、用向量知識回答下列問題:
①四邊形ABCD為矩形的充要條件是______________ ②四邊形ABCD為菱形的充要條件是______________―
3、已知點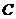 為
為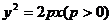 的準線與
的準線與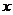 軸的交點,點
軸的交點,點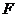 為焦點,點
為焦點,點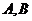 為拋物線上兩個點,若
為拋物線上兩個點,若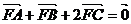 ,則向量
,則向量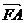 與
與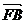 的夾角為
。
的夾角為
。
4、已知平面上不共線的四點O,A,B,C.若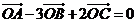 ,則
,則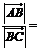 ___ .
___ .
5、設i,j分別是x軸、y軸正方向上的單位向量,且 = 4i-2j,
= 4i-2j,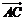 =7i+4j,
=7i+4j,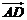 =3i+6j,則四邊形ABCD的面積是________ .
=3i+6j,則四邊形ABCD的面積是________ .
6、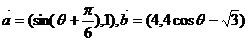 ,若
,若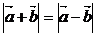 ,則
,則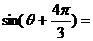 ( )
( )
A. 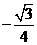 B.
B.
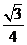 C.
C.
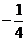 D.
D. 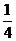
7、過點P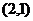 的直線與拋物線
的直線與拋物線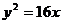 交于
交于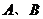 兩點,且
兩點,且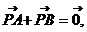 則此直線的方程為___________
則此直線的方程為___________
8.在空間直角坐標系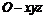 中,過點
中,過點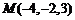 作直線
作直線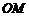 的垂線
的垂線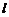 ,則直線
,則直線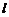 與平面
與平面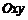 的交點
的交點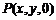 的坐標滿足條件
( )
的坐標滿足條件
( )
A.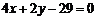 B.
B.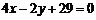
C. D.
D.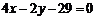
9、已知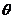 是
是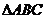 的最大內角,
的最大內角,
(1)向量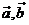 是否共線?說明理由
是否共線?說明理由
(2)定義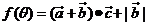 ,求
,求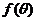 的最大值.
的最大值.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com