
設(shè)函數(shù)![]() 是定義域為R的奇函數(shù).
是定義域為R的奇函數(shù).
(1)求k值;
(2)(文)當![]() 時,試判斷函數(shù)單調(diào)性并求不等式f(x2+2x)+f(x-4)>0的解集;
時,試判斷函數(shù)單調(diào)性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,試判斷函數(shù)單調(diào)性并求使不等式![]() 恒成立的
恒成立的![]() 的取值范圍;
的取值范圍;
(3)若f(1)=![]() ,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值為-2,求m的值.
,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值為-2,求m的值.
解(1)∵f(x)是定義域為R的奇函數(shù),
∴f(0)=0, …………………… 2分
∴1-(k-1)=0,∴k=2, …………………… 4分
(2)(文)
![]()
![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,![]() 單調(diào)遞增,故f(x)在R上單調(diào)遞減。
單調(diào)遞增,故f(x)在R上單調(diào)遞減。
…………………… 6分
原不等式化為:f(x2+2x)>f(4-x)
∴x2+2x<4-x,即x2+3x-4<0 …………………… 8分
∴![]() ,
,
∴不等式的解集為{x|![]() }. …………………………10分
}. …………………………10分
(2)(理)
![]()
![]() ………………6分
………………6分
![]() 單調(diào)遞減,
單調(diào)遞減,![]() 單調(diào)遞增,故f(x)在R上單調(diào)遞減。 ………………7分
單調(diào)遞增,故f(x)在R上單調(diào)遞減。 ………………7分
不等式化為![]()
![]() 恒成立,…………… 8分
恒成立,…………… 8分
![]() ,解得
,解得![]() 。…………………… 10分
。…………………… 10分
(3)∵f(1)=![]() ,
,![]() ,即
,即![]()
![]() ……………………………………12分
……………………………………12分
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x為增函數(shù)
∵x≥1,∴t≥f(1)=![]() ,
,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥![]() )………………15分
)………………15分
若m≥![]() ,當t=m時,h(t)min=2-m2=-2,∴m=2………… 16分
,當t=m時,h(t)min=2-m2=-2,∴m=2………… 16分
若m<![]() ,當t=
,當t=![]() 時,h(t)min=
時,h(t)min=![]() -3m=-2,解得m=
-3m=-2,解得m=![]() >
>![]() ,舍去……17分
,舍去……17分
綜上可知m=2. ………………………………18分


 學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案
學(xué)而優(yōu)暑期銜接南京大學(xué)出版社系列答案 Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業(yè)廣東人民出版社系列答案科目:高中數(shù)學(xué) 來源:2015屆浙江省高一第一次統(tǒng)練數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分10分)設(shè)函數(shù) 是定義域為R的奇函數(shù).
是定義域為R的奇函數(shù).
(1)求 的值;
的值;
(2)若 ,試判斷函數(shù)單調(diào)性(不需證明)并求不等式
,試判斷函數(shù)單調(diào)性(不需證明)并求不等式 的解集;
的解集;
(3)若 上的最小值為
上的最小值為 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆黑龍江省高一上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
設(shè)函數(shù) 是定義域為R的奇函數(shù);
是定義域為R的奇函數(shù);
(Ⅰ)若 ,試求不等式
,試求不等式 的解集;
的解集;
(Ⅱ)若 上的最小值為-2,
上的最小值為-2,
求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:河北省高三下學(xué)期第二次考試數(shù)學(xué)(理) 題型:選擇題
設(shè)函數(shù) 是定義域為R的奇函數(shù),且滿足
是定義域為R的奇函數(shù),且滿足 對一切
對一切 恒成立,當
恒成立,當 時,
時, .則下列四個命題中正確的命題是( )
.則下列四個命題中正確的命題是( )
①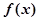 是以4為周期的周期函數(shù);②
是以4為周期的周期函數(shù);②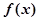 在
在 上的解析式為
上的解析式為 ;
;
③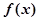 圖象的對稱軸中有
圖象的對稱軸中有 ;④
;④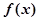 在
在 處的切線方程為
處的切線方程為 .
.
A、①②③ B、②③④ C、①③④ D、①②③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012屆甘肅省高三9月月考理科數(shù)學(xué)試卷 題型:選擇題
設(shè)函數(shù) 是定義域為R的奇函數(shù),且滿足
是定義域為R的奇函數(shù),且滿足 對一切
對一切 恒成立,當
恒成立,當 時,
時, 。則下列四個命題中正確的命題是
。則下列四個命題中正確的命題是
① 是以4為周期的周期函數(shù);②
是以4為周期的周期函數(shù);② 在
在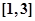 上的解析式為
上的解析式為 ;③
;③ 的圖象的對稱軸中有
的圖象的對稱軸中有 ;④
;④ 在
在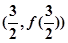 處的切線方程為
處的切線方程為 。
。
A、①②③ B、②③④ C、①③④ D、①②③④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012屆甘肅省高三9月月考文科數(shù)學(xué)試卷 題型:選擇題
設(shè)函數(shù) 是定義域為R的奇函數(shù),且滿足
是定義域為R的奇函數(shù),且滿足 對一切
對一切 恒成立,當
恒成立,當 時,
時, 。則下列四個命題中正確的命題是
。則下列四個命題中正確的命題是
① 是以4為周期的周期函數(shù);②
是以4為周期的周期函數(shù);② 在
在 上的解析式為
上的解析式為 ;③
;③ 的圖象的對稱軸中有
的圖象的對稱軸中有 ;④
;④ 在
在 處的切線方程為
處的切線方程為 。
。
A、①②③ B、②③④ C、①③④ D、①②③④
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com