【題目】2019年，泉州市區的房價依舊是市民關心的話題.總體來說，二手房房價有所下降；相比二手房而言，新房市場依然強勁，價格持續升高.已知銷售人員主要靠售房提成領取工資.現統計泉州市某新房銷售人員2019年一年的工資情況的結果如圖所示，則下列說法正確的是（ ）
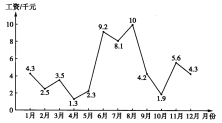
A.2019年該銷售人員月工資的中位數為
B.2019年該銷售人員8月份的工資增長率最高
C.2019年該銷售人員第一季度月工資的方差小于第二季度月工資的方差
D.2019年該銷售人員第一季度月工資的平均數大于第四季度月工資的平均數
科目：高中數學 來源： 題型：
【題目】經統計某射擊運動員隨機射擊一次命中目標的概率為
，為估計該運動員射擊4次恰好命中3次的概率，現采用隨機模擬的方法，先由計算機產生0到9之間取整數值的隨機數，用0，1，2表示沒有擊中，用3，4，5，6，7，8，9表示擊中，以4個隨機數為一組，代表射擊4次的結果，經隨機模擬產生了20組隨機數：
9597，7424，7610，4281，7520，0293，7140，9857，0347，4373，
0371，6233，2616，8045，6011，3661，8638，7815，1457，5550．
根據以上數據，則可估計該運動員射擊4次恰有3次命中的概率為（ ）．
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠生產某種電子產品，每件產品合格的概率均為
，現工廠為提高產品聲譽，要求在交付用戶前每件產品都通過合格檢驗，已知該工廠的檢驗儀器一次最多可檢驗
件該產品，且每件產品檢驗合格與否相互獨立．若每件產品均檢驗一次，所需檢驗費用較多，該工廠提出以下檢驗方案：將產品每
個（
）一組進行分組檢驗，如果某一組產品檢驗合格，則說明該組內產品均合格，若檢驗不合格，則說明該組內有不合格產品，再對該組內每一件產品單獨進行檢驗，如此，每一組產品只需檢驗一次或
次．設該工廠生產
件該產品，記每件產品的平均檢驗次數為
．
（1）的分布列及其期望；
（2）（i）試說明，當越大時，該方案越合理，即所需平均檢驗次數越少；
（ii）當
時，求使該方案最合理時的值及件該產品的平均檢驗次數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐E﹣ABCD的側棱DE與四棱錐F﹣ABCD的側棱BF都與底面ABCD垂直，
，
//
，
.
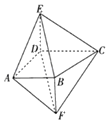
（1）證明：
//平面BCE.
（2）設平面ABF與平面CDF所成的二面角為θ，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2019年泉州市農村電商發展迅猛，成為創新農產品交易方式、增加農民收入、引導農業供給側結構性改革、促進鄉村振興的重要力量，成為鄉村振興的新引擎.2019年大學畢業的李想，選擇回到家鄉泉州自主創業，他在網上開了一家水果網店.2019年雙十一期間，為了增加水果銷量，李想設計了下面兩種促銷方案：方案一：購買金額每滿120元，即可抽獎一次，中獎可獲得20元，每次中獎的概率為
（
），假設每次抽獎相互獨立.方案二：購買金額不低于180元時，即可優惠
元，并在優惠后的基礎上打九折.
（1）在促銷方案一中，設每10個抽獎人次中恰有6人次中獎的概率為
，求的最大值點
；
（2）若促銷方案二中，李想每筆訂單得到的金額均不低于促銷前總價的八折，求的最大值；
（3）以（1）中確定的作為的值，且當取最大值時，若某位顧客一次性購買了360元，則該顧客應選擇哪種促銷方案？請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正態分布有極其廣泛的實際背景，生產與科學實驗中很多隨機變量的概率分布都可以近似地用正態分布來描述.例如，同一種生物體的身長、體重等指標.隨著“綠水青山就是金山銀山”的觀念不斷的深入人心，環保工作快速推進，很多地方的環境出現了可喜的變化.為了調查某水庫的環境保護情況，在水庫中隨機捕撈了100條魚稱重.經整理分析后發現，魚的重量x（單位：kg）近似服從正態分布
，如圖所示，已知
.
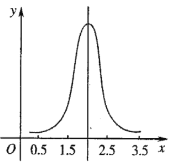
（Ⅰ）若從水庫中隨機捕撈一條魚，求魚的重量在
內的概率；
（Ⅱ）（ⅰ）從捕撈的100條魚中隨機挑出6條魚測量體重，6條魚的重量情況如表.
重量范圍（單位：kg） |
|
|
|
條數 | 1 | 3 | 2 |
為了進一步了解魚的生理指標情況，從6條魚中隨機選出3條，記隨機選出的3條魚中體重在
內的條數為X，求隨機變量X的分布列和數學期望；
（ⅱ）若將選剩下的94條魚稱重做標記后立即放生.兩周后又隨機捕撈1000條魚，發現其中帶有標記的有2條.為了調整生態結構，促進種群的優化，預備捕撈體重在
內的魚的總數的40%進行出售，試估算水庫中魚的條數以及應捕撈體重在內的魚的條數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
+
=1（a＞b＞0）的離心率為
，直線l：x+2y=4與橢圓有且只有一個交點T．
（I）求橢圓C的方程和點T的坐標；
（Ⅱ）O為坐標原點，與OT平行的直線l′與橢圓C交于不同的兩點A，B，直線l′與直線l交于點P，試判斷
是否為定值，若是請求出定值，若不是請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
