
【題目】已知函數![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)在函數![]() 的圖象上任意取定兩點
的圖象上任意取定兩點![]() ,
,![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() ,求證:存在唯一
,求證:存在唯一![]() ,使得
,使得![]() 成立.
成立.
【答案】(Ⅰ)![]() ;(Ⅱ)證明見解析.
;(Ⅱ)證明見解析.
【解析】
(Ⅰ)先對函數求導得![]() ,分類討論
,分類討論![]() 和
和![]() ,利用導數研究函數的單調性和極值,結合
,利用導數研究函數的單調性和極值,結合![]() ,結合極值與最值關系可求出
,結合極值與最值關系可求出![]() 的值;
的值;
(Ⅱ)根據題意,由直線的斜率公式并轉化后得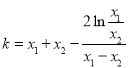 ,構造函數
,構造函數![]() ,并利用導數研究函數
,并利用導數研究函數![]() 的單調性,將證明存在唯一
的單調性,將證明存在唯一![]() ,使得
,使得![]() 成立,轉化為證明不等式
成立,轉化為證明不等式![]() ,
,![]() 即可,分別求出
即可,分別求出![]() 和
和![]() ,再構造函數并根據導數研究單調性和利用導數證明不等式,即可證出.
,再構造函數并根據導數研究單調性和利用導數證明不等式,即可證出.
解:(Ⅰ)由題可知,![]() ,則
,則![]() 的定義域為
的定義域為![]() ,
,
則![]() ,
,
由于![]() ,
,
當![]() 時,因為
時,因為![]() ,所以不滿足題意;
,所以不滿足題意;
當![]() 時,令
時,令![]() ,解得
,解得![]() ,
,
當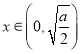 時,
時,![]() ,
,![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
當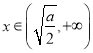 時,
時,![]() ,
,![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
故![]() 是
是![]() 在
在![]() 的唯一最小值點,
的唯一最小值點,
由于![]() ,所以當且僅當
,所以當且僅當![]() ,
,
即![]() 時,
時,![]() ,故
,故![]() .
.
(Ⅱ)由題意知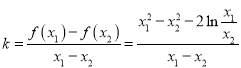
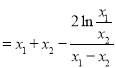 ,
,
令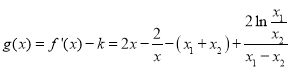 ,
,
則![]() ,故
,故![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
故要證:存在唯一![]() ,使得
,使得![]() 成立,
成立,
只需證:![]() ,
,![]() 即可,
即可,
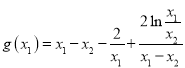
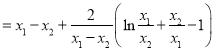 ,
,
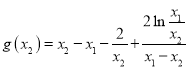
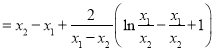 ,
,
令![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() ,
,![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
故![]() ,
,
令![]() 時,有
時,有![]() ,
,
又因為![]() ,
,![]() ,因此
,因此![]() ,
,
由![]() ,令
,令![]() ,得
,得![]() ,
,
令![]() 時,有
時,有![]() ,
,
又因為![]() ,因此
,因此![]() ,
,
綜上,存在唯一![]() ,使得
,使得![]() 成立.
成立.


 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形,![]() ,
,![]() 為
為![]() 上的點,過
上的點,過![]() 的平面分別交
的平面分別交![]() ,
,![]() 于點
于點![]() ,
,![]() ,且
,且![]() 平面
平面![]() .
.
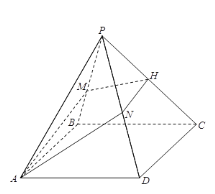
(1)證明:![]() ;
;
(2)當![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某正三棱錐的底面邊長為4,側面與底面所成二面角的余弦值為![]() ,球
,球![]() 為該三棱錐的內切球.球
為該三棱錐的內切球.球![]() 與球
與球![]() 相切,且與該三棱錐的三個側面也相切,則球
相切,且與該三棱錐的三個側面也相切,則球![]() 與球
與球![]() 的表面積之比為( )
的表面積之比為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐![]() 中,頂點
中,頂點![]() 在底面
在底面![]() 的投影為
的投影為![]() 的內心,三個側面的面積分別為12,16,20,且底面面積為24,則三棱錐
的內心,三個側面的面積分別為12,16,20,且底面面積為24,則三棱錐![]() 的內切球的表面積為( )
的內切球的表面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲、乙兩種樹苗中各抽測了10株樹苗的高度,其莖葉圖數據如圖.根據莖葉圖,下列描述正確的是( )
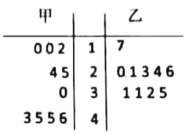
A.甲種樹苗的中位數大于乙種樹苗的中位數,且甲種樹苗比乙種樹苗長得整齊
B.甲種樹苗的中位數大于乙種樹苗的中位數,但乙種樹苗比甲種樹苗長得整齊
C.乙種樹苗的中位數大于甲種樹苗的中位數,且乙種樹苗比甲種樹苗長得整齊
D.乙種樹苗的中位數大于甲種樹苗的中位數,但甲種樹苗比乙種樹苗長得整齊
查看答案和解析>>
科目:高中數學 來源: 題型:
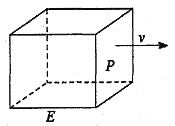
【題目】如圖,長方形物體E在雨中沿面P(面積為S)的垂直方向作勻速移動,速度為![]() ,雨速沿E移動方向的分速度為
,雨速沿E移動方向的分速度為![]() 。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與
。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與![]() ×S成正比,比例系數為
×S成正比,比例系數為![]() ;(2)其它面的淋雨量之和,其值為
;(2)其它面的淋雨量之和,其值為![]() ,記
,記![]() 為E移動過程中的總淋雨量,當移動距離d=100,面積S=
為E移動過程中的總淋雨量,當移動距離d=100,面積S=![]() 時。
時。
(1)寫出![]() 的表達式
的表達式
(2)設0<v≤10,0<c≤5,試根據c的不同取值范圍,確定移動速度![]() ,使總淋雨量
,使總淋雨量![]() 最少。
最少。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年,泉州市區的房價依舊是市民關心的話題.總體來說,二手房房價有所下降;相比二手房而言,新房市場依然強勁,價格持續升高.已知銷售人員主要靠售房提成領取工資.現統計泉州市某新房銷售人員2019年一年的工資情況的結果如圖所示,則下列說法正確的是( )
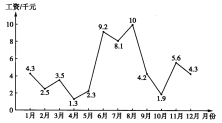
A.2019年該銷售人員月工資的中位數為![]()
B.2019年該銷售人員8月份的工資增長率最高
C.2019年該銷售人員第一季度月工資的方差小于第二季度月工資的方差
D.2019年該銷售人員第一季度月工資的平均數大于第四季度月工資的平均數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com