【題目】本著健康、低碳的生活理念，租自行車騎游的人越來越多.某自行車租車點的收費標準是每車每次租時間不超過兩小時免費，超過兩個小時的部分每小時收費2元（不足1小時的部分按1小時計算）.有甲、乙兩人獨立來該租車點騎游（各組一車一次）.設甲、乙不超過兩小時還車的概率分別為
， 
；兩小時以上且不超過三小時還車的概率分別為
， 
；兩人租車時間都不會超過四小時.
（1）求甲、乙兩人所付租車費用相同的概率；
（2）設甲、乙兩人所付的租車費用之和為隨機變量
，求
的分布列.
【答案】（1）
（2）見解析
【解析】試題分析：（1）由題意可得，甲、乙使用時間情況，
（0，2 | （2，3 | （3，4 | |
甲 |
|
|
|
乙 |
|
|
|
所以車費相同，即使用時間一樣，分成三個互斥事件，有時（0，2
，（2，3
，（3，4
根據互斥事件的和事件和相互獨立事件同時發的概率公式可得
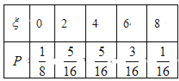
。（2）由題意可得
可能取得值為0，2，4，6，8，其中0元包含（0,0），2元包含（0,2），（2,0），4元包含(0,4),(4,0),(2,2),6元包含(4,2),(2,4), 8元包含(4,4), 根據互斥事件的和事件和相互獨立事件同時發的概率公式分別計算可得。
試題解析：（1）由題意得，甲，乙在三小時以上且不超過四小時還車的概率分別為
， 
．
記甲、乙兩人所付得租車費用相同為事件
．
所以，甲、乙兩人所付得租車費用相同的概率為
．
（2）設甲、乙兩個所付的費用之和為
， 
可能取得值為0，2，4，6，8
， 
， 
，
， 
，
分布列
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）的最小值為1，且f（0）=f（2）=3．
（1）求f（x）的解析式；
（2）若f（x）在區間[2a，a+1]上不單調，求a的取值范圍
（3）若x∈[t，t+2]，試求y=f（x）的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
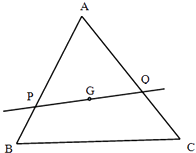
【題目】設G為△ABC的重心，過G作直線l分別交線段AB，AC（不與端點重合）于P，Q．若 
=λ 
， 
=μ 
． 
（1）求 
的值；
（2）求λμ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn ， 且Sn=2n﹣1．數列{bn}滿足b1=2，bn+1﹣2bn=8an ．
（1）求數列{an}的通項公式．
（2）證明：數列{ 
}為等差數列，并求{bn}的通項公式．
（3）求{bn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列關于回歸分析的說法中錯誤的是（ ）
A. 回歸直線一定過樣本中心
B. 殘差圖中殘差點比較均勻地落在水平的帶狀區域中，說明選用的模型比較合適
C. 兩個模型中殘差平方和越小的模型擬合的效果越好
D. 甲、乙兩個模型的
分別約為0.98和0.80，則模型乙的擬合效果更好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某家父母記錄了女兒玥玥的年齡（歲）和身高（單位cm）的數據如下：
年齡x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
（1）試求y關于x的線性回歸方程 
= 
x+ 
（2）試預測玥玥10歲時的身高．（其中， = 
， = 
﹣ 
．
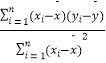查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數{an}：a1=t，n2Sn+1=n2（Sn+an）+an2 ， n=1，2，…．
（1）設{an}為等差數列，且前兩項和S2=3，求t的值；
（2）若t= 
，證明： 
≤an＜1．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
（k＞0）．
（1）若f（x）＞m的解集為{x|x＜﹣3或x＞﹣2}，求不等式5mx2+ 
x+3＞0的解集；
（2）若存在x＞3使得f（x）＞1成立，求k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是等差數列，且a1=2，a1+a2+a3=12．
（1）求數列{an}的通項公式；
（2）令bn=an3n（x∈R）．求數列{bn}前n項和的公式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
